线性微分方程的乌兰型稳定性的莫罕德变换方法
IF 1.3
4区 物理与天体物理
Q3 PHYSICS, MULTIDISCIPLINARY
引用次数: 0
摘要
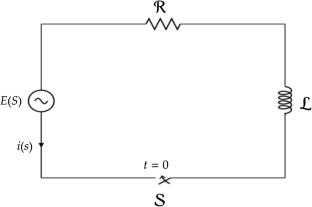
本研究运用莫汉变换方法分析稳定性结果,特别是线性微分方程的 Ulam-Hyers 稳定性。我们对理论结果进行了深入研究,并用拟合良好的实例对其进行了支持。我们还从应用角度出发,利用所提出的方法建立了电路。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Mohand Transform Approach to Ulam-Type Stability of Linear Differential Equations
This study applies the Mohand transform approach to analyze stability results, specifically Ulam-Hyers stability of linear differential equations. We thoroughly examine the theoretical results and support them with well-fitted examples. We also establish the electrical circuit using the proposed method from an application standpoint.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
2.50
自引率
21.40%
发文量
258
审稿时长
3.3 months
期刊介绍:
International Journal of Theoretical Physics publishes original research and reviews in theoretical physics and neighboring fields. Dedicated to the unification of the latest physics research, this journal seeks to map the direction of future research by original work in traditional physics like general relativity, quantum theory with relativistic quantum field theory,as used in particle physics, and by fresh inquiry into quantum measurement theory, and other similarly fundamental areas, e.g. quantum geometry and quantum logic, etc.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


