利用 SPH 框架对颗粒载流进行半拉格朗日模拟
IF 3.6
2区 工程技术
Q1 MECHANICS
International Journal of Multiphase Flow
Pub Date : 2024-10-18
DOI:10.1016/j.ijmultiphaseflow.2024.105033
引用次数: 0
摘要
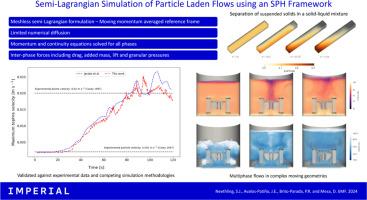
在许多自然和工业系统中都会出现富含颗粒的流动,对其进行模拟尤其具有挑战性。由于平滑粒子流体力学(SPH)和离散元法(DEM)具有共同的拉格朗日性质,因此这两种方法的耦合可以有效地模拟含有粒子的多相流体动力学系统。不过,这种方法也有一些固有的缺点,包括在处理小颗粒时,时间步长过小,令人望而却步。另一种方法是使用欧拉-欧拉参照系,通常使用有限元或有限体积离散法。在这种方法中,每个离散相和连续相的动量和连续性方程都要求解,颗粒则通过浓度场和速度场来模拟。当各相的绝对速度较高而相对速度较低时,这种方法在浓度平流方面会出现较强的数值扩散。这种数值扩散会掩盖行为的重要方面,因为它会使细节变得平滑,特别是在粒子浓度场中。为了减轻这些现有技术的缺点,我们提出了一种基于 SPH 的新半拉格朗日框架,用于求解颗粒载流中所有相的动量和连续性方程。在这个框架中,离散相和连续相相对于以动量平均速度运动的参照系运动。通过关注相对于参照系的速度,与传统的欧拉-欧拉方法相比,我们的方法大大减少了数值扩散,与拉格朗日-拉格朗日方法相比,计算成本更低。通过比较一些相关系统的计算和实验结果,包括倾斜通道中的颗粒-液体分离、液体中的颗粒沉降和气体-颗粒流化床,验证了这种模拟方法。结果表明,这种新方法在结果的准确性和实现结果所需的计算成本方面都非常出色。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Semi-Lagrangian simulation of particle laden flows using an SPH framework
Particle–laden flows occur in many natural and industrial systems and simulating them can be particularly challenging. The coupling of smoothed particle hydrodynamics (SPH) with the discrete element method (DEM) can effectively simulate particle-laden multiphase fluid dynamical systems, due to the shared Lagrangian nature of both methods. However, this approach has some inherent shortcomings, including a prohibitively small time step when dealing with small particles. An alternative approach is to use an Eulerian-Eulerian reference frame, usually using finite element or finite volume discretisations. In this approach, momentum and continuity equations are solved for each discrete phase as well as the continuous phase, and particles are modelled by means of concentration and velocity fields. This approach can suffer from strong numerical diffusion in the advection of the concentrations when absolute velocities of the phases are high, whilst their relative velocities are small. This numerical diffusion can obscure important aspects of the behaviour as it can smooth out details, especially in the particle concentration fields. In order to mitigate the shortcomings of these existing techniques, we present a new SPH-based semi-Lagrangian framework for solving the momentum and continuity equations for all phases in particle-laden flows. In this framework, the discrete and continuous phases move relative to a reference frame that moves at a momentum-averaged velocity. By focusing on velocities relative to the reference frame our method substantially reduces numerical diffusion compared to traditional Eulerian-Eulerian approaches, at a lower computational cost compared to Lagrangian-Lagrangian approaches. The simulation approach is validated by means of comparisons to both computational and experimental results for a number of relevant systems including particle-liquid separation in an inclined channel, particle sedimentation in a liquid, and gas-particle fluidised beds. This new method is shown to compare very favourably in terms of both the accuracy of the results and the computational cost required to achieve them.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
7.30
自引率
10.50%
发文量
244
审稿时长
4 months
期刊介绍:
The International Journal of Multiphase Flow publishes analytical, numerical and experimental articles of lasting interest. The scope of the journal includes all aspects of mass, momentum and energy exchange phenomena among different phases such as occur in disperse flows, gas–liquid and liquid–liquid flows, flows in porous media, boiling, granular flows and others.
The journal publishes full papers, brief communications and conference announcements.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


