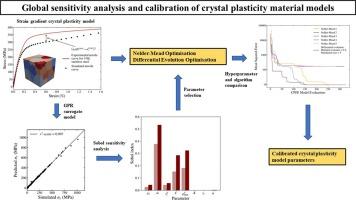
Calibration and surrogate model-based sensitivity analysis of crystal plasticity finite element models

Crystal plasticity models are powerful tools for predicting the deformation behaviour of polycrystalline materials accounting for underlying grain morphology and texture. These models typically have a large number of parameters, an understanding of which is required to effectively calibrate and apply the model. This study presents a structured framework for the global sensitivity analysis of the effect of crystal plasticity parameters on model outputs. Due to the computational cost of evaluating crystal plasticity models multiple times within a finite element framework, a Gaussian process regression surrogate was constructed and used to conduct the sensitivity analysis. Influential parameters from the sensitivity analysis were carried forward for calibration using both a local Nelder-Mead and global differential evolution optimisation algorithm. The results show that the surrogate based global sensitivity analysis is able to efficiently identify influential crystal plasticity parameters and parameter combinations. Comparison of the Nelder-Mead and differential evolution algorithms demonstrated that only the differential evolution algorithm was able to reliably find the global optimum due to the presence of local minima in the calibration objective function. However, the performance of the differential evolution algorithm was dependent on the optimisation hyperparameters selected.