与弗罗贝纽斯换向的傅立叶-穆凯变换

IF 0.8 3区数学 Q2 MATHEMATICS

Bulletin of the London Mathematical Society Pub Date : 2024-09-04 DOI:10.1112/blms.13145

Daniel Bragg

{"title":"与弗罗贝纽斯换向的傅立叶-穆凯变换","authors":"Daniel Bragg","doi":"10.1112/blms.13145","DOIUrl":null,"url":null,"abstract":"We show that a Fourier–Mukai equivalence between smooth projective varieties of characteristic <math>\n <semantics>\n <mi>p</mi>\n <annotation>$p$</annotation>\n </semantics></math> that commutes with either pushforward or pullback along Frobenius is a composition of shifts, isomorphisms, and tensor products with invertible sheaves whose <math>\n <semantics>\n <mrow>\n <mo>(</mo>\n <mi>p</mi>\n <mo>−</mo>\n <mn>1</mn>\n <mo>)</mo>\n </mrow>\n <annotation>$(p-1)$</annotation>\n </semantics></math>th tensor power is trivial.","PeriodicalId":55298,"journal":{"name":"Bulletin of the London Mathematical Society","volume":"56 11","pages":"3477-3483"},"PeriodicalIF":0.8000,"publicationDate":"2024-09-04","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1112/blms.13145","citationCount":"0","resultStr":"{\"title\":\"Fourier–Mukai transforms commuting with Frobenius\",\"authors\":\"Daniel Bragg\",\"doi\":\"10.1112/blms.13145\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"We show that a Fourier–Mukai equivalence between smooth projective varieties of characteristic <math>\\n <semantics>\\n <mi>p</mi>\\n <annotation>$p$</annotation>\\n </semantics></math> that commutes with either pushforward or pullback along Frobenius is a composition of shifts, isomorphisms, and tensor products with invertible sheaves whose <math>\\n <semantics>\\n <mrow>\\n <mo>(</mo>\\n <mi>p</mi>\\n <mo>−</mo>\\n <mn>1</mn>\\n <mo>)</mo>\\n </mrow>\\n <annotation>$(p-1)$</annotation>\\n </semantics></math>th tensor power is trivial.\",\"PeriodicalId\":55298,\"journal\":{\"name\":\"Bulletin of the London Mathematical Society\",\"volume\":\"56 11\",\"pages\":\"3477-3483\"},\"PeriodicalIF\":0.8000,\"publicationDate\":\"2024-09-04\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1112/blms.13145\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Bulletin of the London Mathematical Society\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1112/blms.13145\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Bulletin of the London Mathematical Society","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1112/blms.13145","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

我们证明，特性为 p $p$ 的光滑投影变种之间的傅立叶-穆凯等价关系，与沿弗罗贝纽斯的前推或后拉相通，是移位、同构和张量乘积与可逆剪切的组合，其 ( p - 1 ) $(p-1)$ th 张量幂是微不足道的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

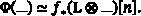
Fourier–Mukai transforms commuting with Frobenius

查看原文本刊更多论文

Fourier–Mukai transforms commuting with Frobenius

We show that a Fourier–Mukai equivalence between smooth projective varieties of characteristic $p$ that commutes with either pushforward or pullback along Frobenius is a composition of shifts, isomorphisms, and tensor products with invertible sheaves whose $(p - 1)$ th tensor power is trivial.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Bulletin of the London Mathematical Society 数学-数学

CiteScore

1.90

自引率

0.00%

发文量

198

审稿时长

4-8 weeks

期刊介绍： Published by Oxford University Press prior to January 2017: http://blms.oxfordjournals.org/