论卢里的∞ $\infty$ -operads 与树枝状的∞ $\infty$ -operads 的等价性

IF 0.8 2区数学 Q2 MATHEMATICS

Journal of Topology Pub Date : 2024-11-01 DOI:10.1112/topo.70003

Vladimir Hinich, Ieke Moerdijk

{"title":"论卢里的∞ $\\infty$ -operads 与树枝状的∞ $\\infty$ -operads 的等价性","authors":"Vladimir Hinich, Ieke Moerdijk","doi":"10.1112/topo.70003","DOIUrl":null,"url":null,"abstract":"In this paper, we prove the equivalence of two symmetric monoidal <math>\n <semantics>\n <mi>∞</mi>\n <annotation>$\\infty$</annotation>\n </semantics></math>-categories of <math>\n <semantics>\n <mi>∞</mi>\n <annotation>$\\infty$</annotation>\n </semantics></math>-operads, the one defined in Lurie [Higher algebra, available at the author's homepage, http://math.ias.edu/~lurie/, September 2017 version] and the one based on dendroidal spaces.","PeriodicalId":56114,"journal":{"name":"Journal of Topology","volume":"17 4","pages":""},"PeriodicalIF":0.8000,"publicationDate":"2024-11-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1112/topo.70003","citationCount":"0","resultStr":"{\"title\":\"On the equivalence of Lurie's \\n \\n ∞\\n $\\\\infty$\\n -operads and dendroidal \\n \\n ∞\\n $\\\\infty$\\n -operads\",\"authors\":\"Vladimir Hinich, Ieke Moerdijk\",\"doi\":\"10.1112/topo.70003\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"In this paper, we prove the equivalence of two symmetric monoidal <math>\\n <semantics>\\n <mi>∞</mi>\\n <annotation>$\\\\infty$</annotation>\\n </semantics></math>-categories of <math>\\n <semantics>\\n <mi>∞</mi>\\n <annotation>$\\\\infty$</annotation>\\n </semantics></math>-operads, the one defined in Lurie [Higher algebra, available at the author's homepage, http://math.ias.edu/~lurie/, September 2017 version] and the one based on dendroidal spaces.\",\"PeriodicalId\":56114,\"journal\":{\"name\":\"Journal of Topology\",\"volume\":\"17 4\",\"pages\":\"\"},\"PeriodicalIF\":0.8000,\"publicationDate\":\"2024-11-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1112/topo.70003\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Topology\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1112/topo.70003\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Topology","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1112/topo.70003","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

在本文中，我们证明了∞ $\infty$ -operads 的两个对称一元∞ $\infty$ -categories 的等价性，一个是 Lurie [高等代数，见作者主页，http://math.ias.edu/~lurie/，2017 年 9 月版]中定义的，另一个是基于树枝状空间的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

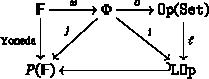
$On the equivalence of Lurie's ∞ $\infty$ -operads and dendroidal ∞ $\infty$ -operads$

查看原文本刊更多论文

On the equivalence of Lurie's ∞ $\infty$ -operads and dendroidal ∞ $\infty$ -operads

In this paper, we prove the equivalence of two symmetric monoidal $\infty$ -categories of $\infty$ -operads, the one defined in Lurie [Higher algebra, available at the author's homepage, http://math.ias.edu/~lurie/, September 2017 version] and the one based on dendroidal spaces.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Topology 数学-数学

CiteScore

2.00

自引率

9.10%

发文量

审稿时长

>12 weeks

期刊介绍： The Journal of Topology publishes papers of high quality and significance in topology, geometry and adjacent areas of mathematics. Interesting, important and often unexpected links connect topology and geometry with many other parts of mathematics, and the editors welcome submissions on exciting new advances concerning such links, as well as those in the core subject areas of the journal. The Journal of Topology was founded in 2008. It is published quarterly with articles published individually online prior to appearing in a printed issue.