具有可变密度和热浓度滑移效应的 MHD 二级纳米流体沿拉伸片热传导的熵优化
IF 6.4
2区 工程技术
Q1 THERMODYNAMICS
引用次数: 0
摘要
本研究的目标是利用外部磁场和温度-浓度滑移效应,探索指数变密度和熵优化对二级纳米流体加热效率和质量-浓度沿扩展表面传输的影响。为了提高纳米粒子的运动和热效率,基于温度的指数形式密度对带磁二级纳米材料的影响是本研究的主要创新点。对于更高的温差,采用了熵优化。利用定义的流函数公式和相似性将领先的二级纳米流体模型转换为常微分形式。采用高效的 Keller box 方法和 Newton Raphson 技术计算数值结果。通过全局矩阵求解未知物理量的最终代数方程。对速度/U 曲线、温度/θ 场、浓度/j 形状、表皮摩擦系数、努塞尔特数和舍伍德数等所有物理约束条件的后果进行了图像和数值分析。使用的参数范围如下 0.1 ≤ ξ ≤ 2.0, 0.0 ≤ n ≤ 1.2, 0.1 ≤ Ec ≤ 2.0, 0.07 ≤ Pr ≤ 7.0, 0.01 ≤ Nt ≤ 0.8, 0.01 ≤ Nb ≤ 0.9。结果发现,随着密度、磁力和温度-滑移约束条件的变化,速度场以最大振幅增加。注意到温度场和浓度场的滑移行为在对流边界条件下有所增加。随着浮力和普朗特系数的增加,局部努塞尔特量和局部舍伍德量也随之增加。本文章由计算机程序翻译,如有差异,请以英文原文为准。
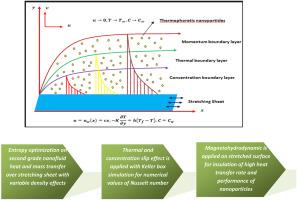
Entropy optimization of MHD second-grade nanofluid thermal transmission along stretched sheet with variable density and thermal-concentration slip effects
The goal of present investigation is to explore the influence of exponential variable density and entropy optimization on second-grade nanofluid heating efficiency and mass-concentration transmission along extended surface using external magnetic-field and temperature-concentration slip effects. To enhance the motion of nanoparticles and thermal efficiency, the influence of exponential form of temperature-based density on magnetically charged second-grade nanomaterial is main novelty of this research. For higher temperature difference, the entropy optimization is used. The defined formulation of stream functions and similarities are used to convert leading second-grade nanofluid model into ordinary differential form. The efficient Keller box method and Newton Raphson technique are applied to compute numerical results. The final algebraic equations are solved through global matrix for unknown physical quantities. The consequence of all physical constraints on velocity/U profile, temperature/θ field, concentration/ϕ shapes, skin friction coefficient, Nusselt and Sherwood number are analyzed pictorially and numerically. The following range of parameters 0.1 ≤ ≤ 2.0, 0.0 ≤ ≤ 1.2, 0.1 ≤ ≤ 2.0, 0.07 ≤ ≤ 7.0, 0.01 ≤ ≤ 0.8, 0.01 ≤ ≤ 0.9 is used. It is found that velocity field increases with maximum amplitude as variable density, magnetic force and temperature-slip constraint. It is noted that the slip behavior in temperature field and concentration field are increased with convective boundary conditions. It is depicted that local Nusselt quantity and local Sherwood quantity increases as buoyancy force and Prandtl coefficient increases.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Case Studies in Thermal Engineering
Chemical Engineering-Fluid Flow and Transfer Processes
CiteScore
8.60
自引率
11.80%
发文量
812
审稿时长
76 days
期刊介绍:
Case Studies in Thermal Engineering provides a forum for the rapid publication of short, structured Case Studies in Thermal Engineering and related Short Communications. It provides an essential compendium of case studies for researchers and practitioners in the field of thermal engineering and others who are interested in aspects of thermal engineering cases that could affect other engineering processes. The journal not only publishes new and novel case studies, but also provides a forum for the publication of high quality descriptions of classic thermal engineering problems. The scope of the journal includes case studies of thermal engineering problems in components, devices and systems using existing experimental and numerical techniques in the areas of mechanical, aerospace, chemical, medical, thermal management for electronics, heat exchangers, regeneration, solar thermal energy, thermal storage, building energy conservation, and power generation. Case studies of thermal problems in other areas will also be considered.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


