边界值问题的神经网络增强可微有限元法
IF 7.1
1区 工程技术
Q1 ENGINEERING, MECHANICAL
International Journal of Mechanical Sciences
Pub Date : 2024-10-16
DOI:10.1016/j.ijmecsci.2024.109783
引用次数: 0
摘要
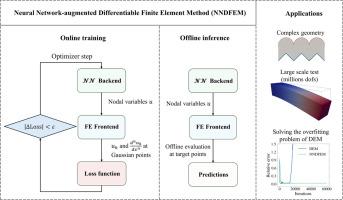
有限元法(FEM)等经典数值方法在解决大规模问题时由于效率较低而受到限制。作为一种新型范例,物理信息神经网络(PINN)在求解偏微分方程方面展现出巨大潜力。然而,传统的 PINN 采用离散采样点的无网格控制,这限制了其有效处理复杂边界的能力。此外,深能量法(DEM,一种特定类型的 PINN)可能会出现灾难性故障。为了应对这些挑战,本研究结合 PINN 和有限元近似,提出了神经网络增强可微有限元法(NNDFEM)。在 NNDFEM 中,神经网络后台只预测节点变量。有限元前端可以很好地处理衍生变量和复杂的边界条件。有限元前端直接执行域上的支配方程、狄里希勒和诺伊曼边界条件。因此,无需在 PINN 中损失边界条件。DEM 中的过拟合问题也得到了显著缓解。全连接神经网络(FCNN)、改进的 FCNN 和图卷积网络作为后端进行了测试。NNDFEM 避免了有限元中的节点力计算和矩阵装配。验证了线性弹性、有限应变非线性弹性、热传导和多孔介质流动的功能损失。系统探索揭示了三维有限元网格的作用。对于大型问题,采用了多保真度学习策略。因此,具有 300 多万自由度的三维案例在两分钟内就能训练有素。得益于神经网络后台的快速推理,前向传递比有限元网格快 8550 倍。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Neural network-augmented differentiable finite element method for boundary value problems
Classical numerical methods such as finite element method (FEM) face limitations due to their low efficiency when addressing large-scale problems. As a novel paradigm, the physics-informed neural network (PINN) has demonstrated significant potential to solve partial differential equations. However, conventional PINNs utilize meshless control at discrete sampling points, which limits their ability to effectively handle complex boundaries. Moreover, catastrophic failure may occur in the deep energy method (DEM, a specific type of PINN). To handle these challenges, this study proposes a Neural Network-augmented Differentiable Finite Element Method (NNDFEM) by combining PINN and finite element approximation. In NNDFEM, the neural network backend solely predicts nodal variables. Derivatives and complex boundary conditions can be well handled by the finite element frontend. The governing equation over the domain, Dirichlet, and Neumann boundary conditions are directly enforced on the finite element frontend. Thus, losses of boundary conditions in PINN are rendered unnecessary. The overfitting problem in DEM is also significantly mitigated. Fully connected neural network (FCNN), modified FCNN, and graph-convolutional network are tested as backends. NNDFEM circumvents nodal force calculation and matrix assembly in FEM. Functional losses of linear elasticity, finite strain nonlinear elasticity, heat conduction, and flow in porous media are validated. A systematic exploration unveils the role of 3D finite element mesh. For large-scale problems, a multi-fidelity learning strategy is employed. Thus, the three-dimensional case with over three million degrees of freedom trains well in two minutes. Benefiting from the fast inference of the neural network backend, the forward pass is 8,550 times faster than FEM.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

International Journal of Mechanical Sciences
工程技术-工程:机械
CiteScore
12.80
自引率
17.80%
发文量
769
审稿时长
19 days
期刊介绍:
The International Journal of Mechanical Sciences (IJMS) serves as a global platform for the publication and dissemination of original research that contributes to a deeper scientific understanding of the fundamental disciplines within mechanical, civil, and material engineering.
The primary focus of IJMS is to showcase innovative and ground-breaking work that utilizes analytical and computational modeling techniques, such as Finite Element Method (FEM), Boundary Element Method (BEM), and mesh-free methods, among others. These modeling methods are applied to diverse fields including rigid-body mechanics (e.g., dynamics, vibration, stability), structural mechanics, metal forming, advanced materials (e.g., metals, composites, cellular, smart) behavior and applications, impact mechanics, strain localization, and other nonlinear effects (e.g., large deflections, plasticity, fracture).
Additionally, IJMS covers the realms of fluid mechanics (both external and internal flows), tribology, thermodynamics, and materials processing. These subjects collectively form the core of the journal's content.
In summary, IJMS provides a prestigious platform for researchers to present their original contributions, shedding light on analytical and computational modeling methods in various areas of mechanical engineering, as well as exploring the behavior and application of advanced materials, fluid mechanics, thermodynamics, and materials processing.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


