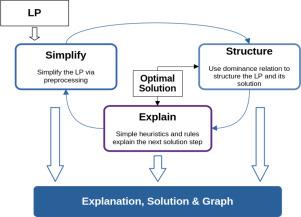
SimplifEx: Simplifying and Explaining Linear Programs

Linear Programming is one of the most common methods for finding optimal solutions to complex problems. Despite its extensive use, solutions are not usually accompanied by explanations, especially explanations for non-experts. Our new tool SimplifEx combines well-known preprocessing techniques with cognitively adequate heuristics to simplify a given linear program, structure its variables, and explain the optimal solution that was found. SimplifEx is meant to improve intuitive understanding of linear programs. In addition, we introduce a generalization of the classical dominance relation in Linear Programming. The order of dominant and dominated variables in an optimal solution can give valuable insights into the structure of a problem and fits well with how humans approach linear programs. The resulting, automatically generated explanations include detailed step-wise listings of processing steps and graphs that provide an overview. The heuristics are based on historical and experimental observations of people solving linear programs by hand. We apply SimplifEx to Stigler’s diet problem as a running example.