合成高度可编程的多稳态克瑞斯林折纸启发单元格
IF 7.1
1区 工程技术
Q1 ENGINEERING, MECHANICAL
International Journal of Mechanical Sciences
Pub Date : 2024-10-03
DOI:10.1016/j.ijmecsci.2024.109768
引用次数: 0
摘要
由于多稳折纸结构能够拥有具有不同特性的多种稳定状态,因此已被用于机械特性定制、可部署机械臂、波传播调谐等领域。传统上,这些结构是通过组装双稳态单元单元制成的,当需要更多稳定状态时,系统的尺寸和重量会显著增加。最近,研究人员在克瑞斯林折纸图案中发现了第三种稳定状态。虽然这是比双稳态单元单元更先进的技术,但仍有机会更系统地扩展克瑞斯林单元单元的设计空间,使其拥有更多的稳定构型(>>2),并增强其可编程多态性。在这项研究中,我们试图开发一种设计克瑞斯林折纸启发单元格的方法,这种单元格可以轻松编程,实现多达 10 种稳定构型,并有可能实现更多构型。我们利用克瑞斯林折纸启发单元单元的丰富运动学特性(源自其耦合的平移和旋转部署),并建议战略性地整合拉伸元素,以实现多种稳定状态。通过分析,我们研究了产生不同数量稳定状态的弦的未拉伸长度值(定义为弦 "松弛 "和 "拉伸 "配置之间的精确长度)。我们展示了双稳态、三稳态、四稳态、五稳态和十稳态单元格的势能曲线及其相应的力位移图。此外,我们还展示了通过简单地调整弦的未拉伸长度,就能对单元格的稳定状态数量进行编程和调整。为了验证所提出的方法,我们设计了三可和五可单元原件并进行了实验测试。最后,我们对串联组装的两个单元格的机械性能定制能力进行了研究。结果表明,可解稳单元电池组件可实现多达 55 个离散的等效刚度值,而双稳态单元电池组件只能实现 3 个等效刚度值。要使双稳态单元单元组件达到这个数值,需要 54 个串联单元单元,这将大大增加结构系统的尺寸和重量。这些研究结果表明,随着每个单元单元稳定状态数量的增加,模块化结构将具有更多的可编程能力,同时将其尺寸和重量保持在最低水平。本文章由计算机程序翻译,如有差异,请以英文原文为准。
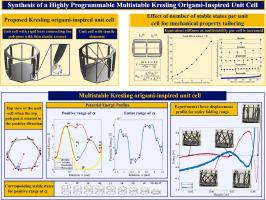
Synthesis of a highly programmable multistable Kresling origami-inspired unit cell
Multistable origami structures have been exploited for mechanical property tailoring, deployable robotic arms, wave propagation tuning and others, due to its ability to possess multiple stable states with distinct properties. Traditionally these structures are made by assembling bistable unit cells, which results in a significant increase in the size and weight of the system when larger number of stable states are required. Recently, researchers have uncovered a third stable state in the Kresling origami pattern. Although this is an advancement over the bistable unit cell, there is an unexplored opportunity for more systematically expanding the design space of Kresling unit cells to possess many more stable configurations (>>2) and enhance its programmable multistability. In this research, we seek to develop a methodology for the design of a Kresling origami-inspired unit cell that can be easily programmed to achieve up to 10 stable configurations, with the potential to achieve even more. We exploit the rich kinematics of the Kresling origami-inspired unit cell, that arise from its coupled translational and rotational deployment, and propose the strategic integration of tensile elements to realize multiple stable states. Analytically, we study the unstretched length values (defined to be the precise length between the string “slacked” and “tensioned” configurations) of the strings that yield the distinct number of stable states. We present the potential energy profiles with its corresponding force-displacement plots for the bistable, tristable, quadstable, pentastable and decastable unit cells. Moreover, we show that by simply adjusting the unstretched length of the strings we can program and tune the number of stable states of the unit cell. Tristable and pentastable unit cell prototypes are designed and experimentally tested to validate the proposed methodology. Lastly, a study is performed on the mechanical property tailoring capabilities of two unit cells assembled in series. The results show that the decastable unit cell assembly can achieve up to 55 discrete values of equivalent stiffness, while the bistable one can only achieve 3. For the bistable unit cell assembly to match this number, it will require 54 unit cells in series, which will significantly increase the size and weight of the structural system. These findings show that the modular structure will have more programmable capabilities, while maintaining its size and weight at a minimum, as the number of stable states per unit cell is increased.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

International Journal of Mechanical Sciences
工程技术-工程:机械
CiteScore
12.80
自引率
17.80%
发文量
769
审稿时长
19 days
期刊介绍:
The International Journal of Mechanical Sciences (IJMS) serves as a global platform for the publication and dissemination of original research that contributes to a deeper scientific understanding of the fundamental disciplines within mechanical, civil, and material engineering.
The primary focus of IJMS is to showcase innovative and ground-breaking work that utilizes analytical and computational modeling techniques, such as Finite Element Method (FEM), Boundary Element Method (BEM), and mesh-free methods, among others. These modeling methods are applied to diverse fields including rigid-body mechanics (e.g., dynamics, vibration, stability), structural mechanics, metal forming, advanced materials (e.g., metals, composites, cellular, smart) behavior and applications, impact mechanics, strain localization, and other nonlinear effects (e.g., large deflections, plasticity, fracture).
Additionally, IJMS covers the realms of fluid mechanics (both external and internal flows), tribology, thermodynamics, and materials processing. These subjects collectively form the core of the journal's content.
In summary, IJMS provides a prestigious platform for researchers to present their original contributions, shedding light on analytical and computational modeling methods in various areas of mechanical engineering, as well as exploring the behavior and application of advanced materials, fluid mechanics, thermodynamics, and materials processing.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


