通过弗罗贝尼斯结构定理比较非阿基米德和对数镜像构造
IF 1
2区 数学
Q1 MATHEMATICS
Journal of the London Mathematical Society-Second Series
Pub Date : 2024-10-25
DOI:10.1112/jlms.12998
引用次数: 0
摘要
对于 X ∖ D $X\setminus D$ 平滑仿射的 log Calabi Yau 对 ( X , D $X,D$ ),满足最大退化假设或包含一个扎里斯基致密环,我们证明在 D 是一个 nef 除数的支持的条件下,由 Gross-Siebert 构造的镜像代数上定义迹形式的结构常数是由 Keel-Yu 定义的天真曲线计数给出的。作为推论,我们推导出,在 X ∖ D $X\setminus D$ 的情况下,格罗斯-西贝特和基尔-尤构建的镜像代数的相等性包含一个扎里斯基致密环。此外,我们还利用这一结果证明了曼德尔针对满足最大退化假设的法诺对提出的镜像猜想。本文章由计算机程序翻译,如有差异,请以英文原文为准。
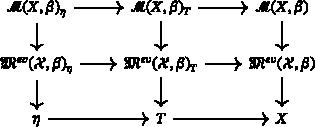
Comparison of nonarchimedean and logarithmic mirror constructions via the Frobenius structure theorem
For a log Calabi Yau pair () with smooth affine, satisfying either a maximal degeneracy assumption or contains a Zariski dense torus, we prove under the condition that D is the support of a nef divisor that the structure constants defining a trace form on the mirror algebra constructed by Gross–Siebert are given by the naive curve counts defined by Keel–Yu. As a corollary, we deduce that the equality of the mirror algebras constructed by Gross–Siebert and Keel–Yu in the case contains a Zariski dense torus. In addition, we use this result to prove a mirror conjecture proposed by Mandel for Fano pairs satisfying the maximal degeneracy assumption.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.90
自引率
0.00%
发文量
186
审稿时长
6-12 weeks
期刊介绍:
The Journal of the London Mathematical Society has been publishing leading research in a broad range of mathematical subject areas since 1926. The Journal welcomes papers on subjects of general interest that represent a significant advance in mathematical knowledge, as well as submissions that are deemed to stimulate new interest and research activity.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


