使用密度矩阵重正化群法的极性化学
IF 5.7
1区 化学
Q2 CHEMISTRY, PHYSICAL
引用次数: 0
摘要
新兴的极性化学领域探索分子在空腔模式强耦合下的行为。尽管模拟电子强耦合下极性化学的 ab initio 极性方法取得了最新发展,但其能力仍然有限,尤其是在分子还具有强电子相关性的情况下。为了弥补这一差距,我们开发了一种新颖的空腔 QED 计算方法,利用密度矩阵重正化组(DMRG)算法和保利-菲尔兹哈密顿方程。我们采用这种方法研究了空穴对 n-oligoacenes 的 S0-S1 转变的影响,n 从 2 到 5 不等,在最大的并五苯分子中包含 22 个完全相关的 π 轨道。我们的研究结果表明,空腔的影响随着烯的增大而增强。此外,我们还证明,与完全行列式表示法不同,DMRG 有效地优化并消除了多余的光子自由度,从而使计算成本随着光子基的增加而逐渐不变。本文章由计算机程序翻译,如有差异,请以英文原文为准。
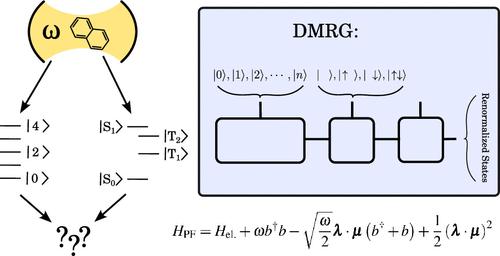
Polaritonic Chemistry Using the Density Matrix Renormalization Group Method
The emerging field of polaritonic chemistry explores the behavior of molecules under strong coupling with cavity modes. Despite recent developments in ab initio polaritonic methods for simulating polaritonic chemistry under electronic strong coupling, their capabilities are limited, especially in cases where the molecule also features strong electronic correlation. To bridge this gap, we have developed a novel method for cavity QED calculations utilizing the Density Matrix Renormalization Group (DMRG) algorithm in conjunction with the Pauli–Fierz Hamiltonian. Our approach is applied to investigate the effect of the cavity on the S0–S1 transition of n-oligoacenes, with n ranging from 2 to 5, encompassing 22 fully correlated π orbitals in the largest pentacene molecule. Our findings indicate that the influence of the cavity intensifies with larger acenes. Additionally, we demonstrate that, unlike the full determinantal representation, DMRG efficiently optimizes and eliminates excess photonic degrees of freedom, resulting in an asymptotically constant computational cost as the photonic basis increases.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Journal of Chemical Theory and Computation
化学-物理:原子、分子和化学物理
CiteScore
9.90
自引率
16.40%
发文量
568
审稿时长
1 months
期刊介绍:
The Journal of Chemical Theory and Computation invites new and original contributions with the understanding that, if accepted, they will not be published elsewhere. Papers reporting new theories, methodology, and/or important applications in quantum electronic structure, molecular dynamics, and statistical mechanics are appropriate for submission to this Journal. Specific topics include advances in or applications of ab initio quantum mechanics, density functional theory, design and properties of new materials, surface science, Monte Carlo simulations, solvation models, QM/MM calculations, biomolecular structure prediction, and molecular dynamics in the broadest sense including gas-phase dynamics, ab initio dynamics, biomolecular dynamics, and protein folding. The Journal does not consider papers that are straightforward applications of known methods including DFT and molecular dynamics. The Journal favors submissions that include advances in theory or methodology with applications to compelling problems.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


