稀拉顿黑洞中离散变量和连续变量的守恒互信息
IF 4.6
2区 物理与天体物理
Q1 PHYSICS, MULTIDISCIPLINARY
引用次数: 0
摘要
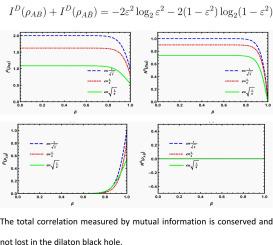
黑洞的信息悖论一直是理论物理学前沿的热门话题。本文旨在从初始子系统 A 和 B 之间以互信息量化的总相关性的角度来理解稀拉顿黑洞的信息悖论。我们发现,稀拉顿引力可以重新分配子系统 A 和 B 之间离散变量和连续变量的初始互信息,但不能重新分配初始纠缠。有趣的是,物理上可获取的互信息与不可获取的互信息之和等于初始互信息。因此,在黑洞的稀释引力作用下,物理上可获取的互信息会转化为物理上不可获取的互信息。从互信息的角度来看,黑洞的信息是守恒的,不会丢失。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Conserved mutual information for discrete and continuous variables in dilaton black hole
The information paradox of black holes has always been a hot topic at the forefront of theoretical physics. In this paper, we aim to understand the information paradox of the dilaton black hole from the perspective of the total correlation quantified by mutual information between the initial subsystems and . We find that the dilaton gravity can redistribute initial mutual information for discrete and continuous variables between the subsystems and , but cannot redistribute initial entanglement. Interestingly, the sum of physically accessible and inaccessible mutual information is equal to the initial mutual information. Therefore, physically accessible mutual information is transformed into physically inaccessible mutual information by the dilaton gravity of the black hole. From the perspective of mutual information, the information of black holes is conserved and not lost.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Chinese Journal of Physics
物理-物理:综合
CiteScore
8.50
自引率
10.00%
发文量
361
审稿时长
44 days
期刊介绍:
The Chinese Journal of Physics publishes important advances in various branches in physics, including statistical and biophysical physics, condensed matter physics, atomic/molecular physics, optics, particle physics and nuclear physics.
The editors welcome manuscripts on:
-General Physics: Statistical and Quantum Mechanics, etc.-
Gravitation and Astrophysics-
Elementary Particles and Fields-
Nuclear Physics-
Atomic, Molecular, and Optical Physics-
Quantum Information and Quantum Computation-
Fluid Dynamics, Nonlinear Dynamics, Chaos, and Complex Networks-
Plasma and Beam Physics-
Condensed Matter: Structure, etc.-
Condensed Matter: Electronic Properties, etc.-
Polymer, Soft Matter, Biological, and Interdisciplinary Physics.
CJP publishes regular research papers, feature articles and review papers.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


