具有符号切换和不连续泊松比的超材料
IF 3.4
3区 工程技术
Q1 MECHANICS
International Journal of Solids and Structures
Pub Date : 2024-10-09
DOI:10.1016/j.ijsolstr.2024.113095
引用次数: 0
摘要
最近的研究表明,碎裂-重构(FR)超材料是在原始状态下产生泊松比不连续的合适候选材料。本文介绍了一种新的碎裂-重构超材料,它还允许在沿一条轴线发生应力反转时实现泊松比的符号转换。这是通过使用旋转菱形来实现的,其中每个菱形可进一步分割成六个子单元。后者由两个不旋转的较小菱形和四个旋转的等腰三角形组成。结果表明,由于机制不同,超材料在沿一条轴线发生应力反转时,泊松比会发生符号转换,但在沿另一条轴线方向加载时,由于该方向的尺寸最大,泊松比却不会发生符号转换。相反,有两种压缩途径可导致破碎或重组变形模式。每种途径的倾向性都是通过电荷附着物提出的。这种超材料的独特性使其可以应用于其他材料和超材料无法实现的领域。本文章由计算机程序翻译,如有差异,请以英文原文为准。
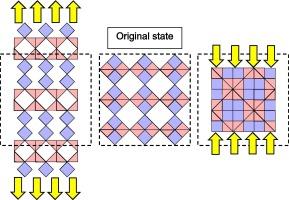
A metamaterial with sign-switching and discontinuous Poisson’s ratio
The fragmentation-reconstitution (FR) metamaterial has recently been shown to be a suitable candidate for producing Poisson’s ratio discontinuity at the original state. A new FR metamaterial is introduced herein that additionally permits sign-switching of Poisson’s ratio upon stress reversal along one axis. This was achieved by the use of rotating rhombi in which every rhombus can be further fragmented into six sub-units. The latter consists of two non-rotating smaller rhombi and four rotating isosceles triangles. While results show that the metamaterial exhibits sign-switching of Poisson’s ratio upon stress reversal along one axis due to differing mechanism, this is not so for loading in the other on-axis direction due to the dimension being maximum in that direction. Instead, there are two compression pathways which can lead to either fragmentation or reconstitution modes of deformation. The predisposition for each pathway is proposed by means of charge attachments. The uniqueness of this metamaterial avails its use for applications that are not attainable by other materials and metamaterials.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
6.70
自引率
8.30%
发文量
405
审稿时长
70 days
期刊介绍:
The International Journal of Solids and Structures has as its objective the publication and dissemination of original research in Mechanics of Solids and Structures as a field of Applied Science and Engineering. It fosters thus the exchange of ideas among workers in different parts of the world and also among workers who emphasize different aspects of the foundations and applications of the field.
Standing as it does at the cross-roads of Materials Science, Life Sciences, Mathematics, Physics and Engineering Design, the Mechanics of Solids and Structures is experiencing considerable growth as a result of recent technological advances. The Journal, by providing an international medium of communication, is encouraging this growth and is encompassing all aspects of the field from the more classical problems of structural analysis to mechanics of solids continually interacting with other media and including fracture, flow, wave propagation, heat transfer, thermal effects in solids, optimum design methods, model analysis, structural topology and numerical techniques. Interest extends to both inorganic and organic solids and structures.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


