细胞自动机综合分类法
IF 3.4
2区 数学
Q1 MATHEMATICS, APPLIED
Communications in Nonlinear Science and Numerical Simulation
Pub Date : 2024-09-21
DOI:10.1016/j.cnsns.2024.108362
引用次数: 0
摘要
细胞自动机(CA)是一种完全离散的动力学模型,由于其相对简单的设置却能表达高度复杂的现象,因而受到广泛关注。尽管该模型理论成熟、计算能力强大,但目前缺乏对各种细胞自动机族 "分类 "的完整调查,这阻碍了高效的跨学科研究进展。这篇综述论文弥补了这一不足;它有条不紊地概述了五个重要的 CA "族":异步 CA、随机 CA、多状态 CA、扩展邻域 CA 和非均匀 CA。随后从四个角度介绍了这五个 CA 系列。首先,给出严格的数学定义。其次,我们绘制了每个 CA 族中的突出变体,从而突出了与其他族类型的数学等价性。第三,我们通过数学工具讨论这些 CA 类型的基因型和表型,并指出既定工具何时失效。第四,我们在每一节的最后简要概述了与信息论和数学建模相关的应用。本文章由计算机程序翻译,如有差异,请以英文原文为准。
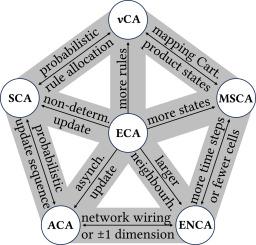
A comprehensive taxonomy of cellular automata
Cellular automata (CAs) are fully-discrete dynamical models that have received much attention due to the fact that their relatively simple setup can nonetheless express highly complex phenomena. Despite the model’s theoretical maturity and abundant computational power, the current lack of a complete survey on the ‘taxonomy’ of various families of CAs impedes efficient and interdisciplinary progress. This review paper mitigates that deficiency; it provides a methodical overview of five important CA ‘families’: asynchronous, stochastic, multi-state, extended-neighbourhood, and non-uniform CAs. These five CA families are subsequently presented from four angles. First, a rigorous mathematical definition is given. Second, we map prominent variations within each CA family, as such highlighting mathematical equivalences with types from other families. Third, we discuss the genotype and phenotype of these CA types by means of mathematical tools, indicating when established tools break down. Fourth, we conclude each section with a brief overview of applications related to information theory and mathematical modelling.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Communications in Nonlinear Science and Numerical Simulation
MATHEMATICS, APPLIED-MATHEMATICS, INTERDISCIPLINARY APPLICATIONS
CiteScore
6.80
自引率
7.70%
发文量
378
审稿时长
78 days
期刊介绍:
The journal publishes original research findings on experimental observation, mathematical modeling, theoretical analysis and numerical simulation, for more accurate description, better prediction or novel application, of nonlinear phenomena in science and engineering. It offers a venue for researchers to make rapid exchange of ideas and techniques in nonlinear science and complexity.
The submission of manuscripts with cross-disciplinary approaches in nonlinear science and complexity is particularly encouraged.
Topics of interest:
Nonlinear differential or delay equations, Lie group analysis and asymptotic methods, Discontinuous systems, Fractals, Fractional calculus and dynamics, Nonlinear effects in quantum mechanics, Nonlinear stochastic processes, Experimental nonlinear science, Time-series and signal analysis, Computational methods and simulations in nonlinear science and engineering, Control of dynamical systems, Synchronization, Lyapunov analysis, High-dimensional chaos and turbulence, Chaos in Hamiltonian systems, Integrable systems and solitons, Collective behavior in many-body systems, Biological physics and networks, Nonlinear mechanical systems, Complex systems and complexity.
No length limitation for contributions is set, but only concisely written manuscripts are published. Brief papers are published on the basis of Rapid Communications. Discussions of previously published papers are welcome.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


