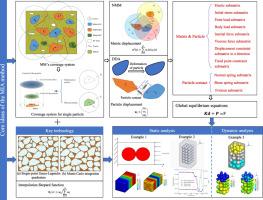
A continuous-discontinuous coupling computational method for multi-material mixtures

Considering the important role of particle-reinforced composites (PRCs), and to accurately assess the mechanical properties of PRC with arbitrarily complex internal structures, this paper proposes a new continuous-discontinuous coupled computational method, i.e., the multi-material integrated analysis (MIA) method, by combining the advantages of the discontinuous deformation analysis (DDA) method, the numerical manifold method (NMM), and the meshless method, for the continuous-discontinuous dual state of this kind of materials when they are subjected to forces. The core idea of this method is by establishing a single physical cover (PC) on each particle and defining a unified and piecewise approximation function over it to achieve displacement coordination between the particles and the matrix. In this model, the particles can maintain the contact and separation characteristics like the blocks, while the matrix is able to achieve the bonding function by overlapping different covers. Two numerical integration schemes, namely single-point Gaussian integration and Monte Carlo integration, are proposed to address the integration issues in stiffness matrix calculations. Meanwhile by considering the similarity between NMM and meshless method interpolation function construction, this paper combines circular coverage and 0th-order moving least squares to construct the interpolation function to form the displacement approximation function for the whole solution space. Moreover, the method of lattice retrieval (also Nearest Neighbor Search, NNS) is invoked for particle contact determination to improve the efficiency of contact and coverage relationship determination. The validity of the model is verified by taking asphalt mixture, a typical PRC, as a demonstrative case study. The results show that the MIA method solves the one-sided problem that the existing algorithms usually only consider the continuous or discontinuous properties of PRC, and provides a new method for comprehensively analyzing the micromechanical response of PRC and solving its large deformation problem.