具有可变形正弦-戈登形状的基底电势中的参数诱导逻辑随机共振
IF 4.6
2区 物理与天体物理
Q1 PHYSICS, MULTIDISCIPLINARY
引用次数: 0
摘要
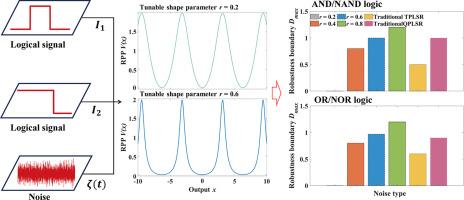
逻辑随机共振(LSR)系统是一种物理非线性系统,能够在噪声影响下进行稳健的布尔逻辑运算。虽然适合电子电路实现的 LSR 系统已被广泛研究,但凝聚态 LSR 系统的研究仍局限于具有饱和特性的受限双稳态。考虑到许多物理系统中存在周期性非线性,本研究首次提出了一种基于可变形正弦-戈登形雷莫森内-佩拉尔电势(RPP)的 LSR 系统。在无噪声和有噪声条件下进行的测试证明,在所提出的系统中存在参数诱导的 LSR 现象。此外,我们还发现,相对较宽的势阱形状有助于增强基于 RPP 的 LSR 系统的噪声鲁棒性。此外,我们还将传统的基于多项式非线性的 LSR 系统与所提出的系统进行了比较。无论噪声是高斯白噪声还是包含尖峰脉冲的复合噪声,基于 RPP 的 LSR 系统都表现出卓越的鲁棒性。这些结果证明了基于 RPP 的 LSR 系统的独特优势,并鼓励进一步设计基于可变形周期非线性的凝聚态 LSR 系统。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Parameter-induced logical stochastic resonance in substrate potential with deformable sine-Gordon shape
Logical stochastic resonance (LSR) systems are physical nonlinear systems capable of robust Boolean logic operations under the influence of noise. While LSR systems suitable for electronic circuit implementation have been extensively studied, research on condensed matter LSR systems remains limited to constrained bistability with saturation characteristic. Considering the presence of periodic nonlinearities in many physical systems, a deformable sine-Gordon-shaped Remoissenet–Peyrard potential (RPP)-based LSR system is proposed for the first time in this work. Testing under both noise-free and noisy conditions proves the existence of parameter-induced LSR phenomena in the proposed system. Moreover, we find that a relatively wide potential well shape contributes to enhanced noise robustness in the RPP-based LSR system. Additionally, traditional polynomial nonlinearity-based LSR systems are compared with the proposed system. Regardless of whether the noise is Gaussian white noise or composite noise containing spiking pulses, the RPP-based LSR system exhibits superior robustness. The results demonstrate the exceptional advantages of the RPP-based LSR system and encourage further design of condensed matter LSR systems based on deformable periodic nonlinearities.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Chinese Journal of Physics
物理-物理:综合
CiteScore
8.50
自引率
10.00%
发文量
361
审稿时长
44 days
期刊介绍:
The Chinese Journal of Physics publishes important advances in various branches in physics, including statistical and biophysical physics, condensed matter physics, atomic/molecular physics, optics, particle physics and nuclear physics.
The editors welcome manuscripts on:
-General Physics: Statistical and Quantum Mechanics, etc.-
Gravitation and Astrophysics-
Elementary Particles and Fields-
Nuclear Physics-
Atomic, Molecular, and Optical Physics-
Quantum Information and Quantum Computation-
Fluid Dynamics, Nonlinear Dynamics, Chaos, and Complex Networks-
Plasma and Beam Physics-
Condensed Matter: Structure, etc.-
Condensed Matter: Electronic Properties, etc.-
Polymer, Soft Matter, Biological, and Interdisciplinary Physics.
CJP publishes regular research papers, feature articles and review papers.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


