用米库辛斯基代数微积分分析放射性衰变中的多期分数贝特曼方程

IF 4.6 2区物理与天体物理 Q1 PHYSICS, MULTIDISCIPLINARY

Chinese Journal of Physics Pub Date : 2024-10-09 DOI:10.1016/j.cjph.2024.10.002

Marc Jornet

{"title":"用米库辛斯基代数微积分分析放射性衰变中的多期分数贝特曼方程","authors":"Marc Jornet","doi":"10.1016/j.cjph.2024.10.002","DOIUrl":null,"url":null,"abstract":"<div><div>Fractional Bateman equations model the concentrations of nuclear species through a radioactive decay chain, by considering non-Markovian behavior. Cruz-López and Espinosa-Paredes (Nuclear Engineering and Technology, 2022) solved the mathematical problem with a single memory coefficient, based on the Laplace-transform technique. Cruz-López, Espinosa-Paredes and François (Computer Physics Communications, 2022) extended the analysis to several fractional orders, with Laplace transforms and series expansions checked by induction. In this paper, we solve such a case of distinct memory effects, via the more general method of Mikusiński operational calculus. We do not distinguish between equal and different decay rates. Multivariate Mittag-Leffler functions appear in the closed-form expression.</div></div>","PeriodicalId":10340,"journal":{"name":"Chinese Journal of Physics","volume":null,"pages":null},"PeriodicalIF":4.6000,"publicationDate":"2024-10-09","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Analysis of the multi-term fractional Bateman equations in radioactive decay by means of Mikusiński algebraic calculus\",\"authors\":\"Marc Jornet\",\"doi\":\"10.1016/j.cjph.2024.10.002\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><div>Fractional Bateman equations model the concentrations of nuclear species through a radioactive decay chain, by considering non-Markovian behavior. Cruz-López and Espinosa-Paredes (Nuclear Engineering and Technology, 2022) solved the mathematical problem with a single memory coefficient, based on the Laplace-transform technique. Cruz-López, Espinosa-Paredes and François (Computer Physics Communications, 2022) extended the analysis to several fractional orders, with Laplace transforms and series expansions checked by induction. In this paper, we solve such a case of distinct memory effects, via the more general method of Mikusiński operational calculus. We do not distinguish between equal and different decay rates. Multivariate Mittag-Leffler functions appear in the closed-form expression.</div></div>\",\"PeriodicalId\":10340,\"journal\":{\"name\":\"Chinese Journal of Physics\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":4.6000,\"publicationDate\":\"2024-10-09\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Chinese Journal of Physics\",\"FirstCategoryId\":\"101\",\"ListUrlMain\":\"https://www.sciencedirect.com/science/article/pii/S0577907324003927\",\"RegionNum\":2,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"PHYSICS, MULTIDISCIPLINARY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Chinese Journal of Physics","FirstCategoryId":"101","ListUrlMain":"https://www.sciencedirect.com/science/article/pii/S0577907324003927","RegionNum":2,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"PHYSICS, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

摘要

分数贝特曼方程通过考虑非马尔可夫行为，对放射性衰变链中的核物种浓度进行建模。克鲁兹-洛佩斯和埃斯皮诺萨-帕雷德斯（核工程与技术，2022 年）基于拉普拉斯变换技术，用单一记忆系数解决了这一数学问题。克鲁兹-洛佩斯、埃斯皮诺萨-帕雷德斯和弗朗索瓦（《计算机物理通讯》，2022 年）将分析扩展到多个分数阶，通过归纳法检验拉普拉斯变换和数列展开。在本文中，我们通过米库辛斯基运算微积分的更一般方法，解决了这种不同记忆效应的情况。我们不区分相同和不同的衰减率。多变量米塔格-勒弗勒函数出现在闭式表达式中。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

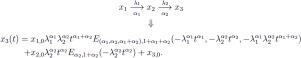
$Analysis of the multi-term fractional Bateman equations in radioactive decay by means of Mikusiński algebraic calculus$

查看原文本刊更多论文

Analysis of the multi-term fractional Bateman equations in radioactive decay by means of Mikusiński algebraic calculus

Fractional Bateman equations model the concentrations of nuclear species through a radioactive decay chain, by considering non-Markovian behavior. Cruz-López and Espinosa-Paredes (Nuclear Engineering and Technology, 2022) solved the mathematical problem with a single memory coefficient, based on the Laplace-transform technique. Cruz-López, Espinosa-Paredes and François (Computer Physics Communications, 2022) extended the analysis to several fractional orders, with Laplace transforms and series expansions checked by induction. In this paper, we solve such a case of distinct memory effects, via the more general method of Mikusiński operational calculus. We do not distinguish between equal and different decay rates. Multivariate Mittag-Leffler functions appear in the closed-form expression.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Chinese Journal of Physics 物理-物理：综合

CiteScore

8.50

自引率

10.00%

发文量

361

审稿时长

44 days

期刊介绍： The Chinese Journal of Physics publishes important advances in various branches in physics, including statistical and biophysical physics, condensed matter physics, atomic/molecular physics, optics, particle physics and nuclear physics. The editors welcome manuscripts on: -General Physics: Statistical and Quantum Mechanics, etc.- Gravitation and Astrophysics- Elementary Particles and Fields- Nuclear Physics- Atomic, Molecular, and Optical Physics- Quantum Information and Quantum Computation- Fluid Dynamics, Nonlinear Dynamics, Chaos, and Complex Networks- Plasma and Beam Physics- Condensed Matter: Structure, etc.- Condensed Matter: Electronic Properties, etc.- Polymer, Soft Matter, Biological, and Interdisciplinary Physics. CJP publishes regular research papers, feature articles and review papers.