具有对称 Hulthén 势的 Dunkl-Schrödinger 方程的近似边界状态

IF 1.7 4区物理与天体物理 Q2 PHYSICS, MULTIDISCIPLINARY

Few-Body Systems Pub Date : 2024-09-24 DOI:10.1007/s00601-024-01960-y

Axel Schulze-Halberg

{"title":"具有对称 Hulthén 势的 Dunkl-Schrödinger 方程的近似边界状态","authors":"Axel Schulze-Halberg","doi":"10.1007/s00601-024-01960-y","DOIUrl":null,"url":null,"abstract":"<div><p>We construct approximate bound state solutions to the one-dimensional Schrödinger equation within the Dunkl formalism for a symmetrized Hulthén potential. Our method is based on reducing the governing equation to conventional Schrödinger form, such that an approximation to an inverse quadratic term becomes applicable. Conditions for computing stationary energies, as well as for establishing boundedness and normalizability of our solutions are discussed.</p></div>","PeriodicalId":556,"journal":{"name":"Few-Body Systems","volume":"65 4","pages":""},"PeriodicalIF":1.7000,"publicationDate":"2024-09-24","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Approximate Bound States for the Dunkl–Schrödinger Equation with Symmetrized Hulthén Potential\",\"authors\":\"Axel Schulze-Halberg\",\"doi\":\"10.1007/s00601-024-01960-y\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>We construct approximate bound state solutions to the one-dimensional Schrödinger equation within the Dunkl formalism for a symmetrized Hulthén potential. Our method is based on reducing the governing equation to conventional Schrödinger form, such that an approximation to an inverse quadratic term becomes applicable. Conditions for computing stationary energies, as well as for establishing boundedness and normalizability of our solutions are discussed.</p></div>\",\"PeriodicalId\":556,\"journal\":{\"name\":\"Few-Body Systems\",\"volume\":\"65 4\",\"pages\":\"\"},\"PeriodicalIF\":1.7000,\"publicationDate\":\"2024-09-24\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Few-Body Systems\",\"FirstCategoryId\":\"101\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s00601-024-01960-y\",\"RegionNum\":4,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"PHYSICS, MULTIDISCIPLINARY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Few-Body Systems","FirstCategoryId":"101","ListUrlMain":"https://link.springer.com/article/10.1007/s00601-024-01960-y","RegionNum":4,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"PHYSICS, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

摘要

我们在 Dunkl 形式中构建了对称 Hulthén 势的一维薛定谔方程的近似边界解。我们的方法基于将支配方程还原为常规薛定谔形式，从而使反二次项的近似值变得适用。我们讨论了计算静态能量的条件，以及建立我们的解的有界性和可归一化性的条件。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

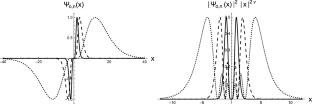
Approximate Bound States for the Dunkl–Schrödinger Equation with Symmetrized Hulthén Potential

查看原文本刊更多论文

Approximate Bound States for the Dunkl–Schrödinger Equation with Symmetrized Hulthén Potential

We construct approximate bound state solutions to the one-dimensional Schrödinger equation within the Dunkl formalism for a symmetrized Hulthén potential. Our method is based on reducing the governing equation to conventional Schrödinger form, such that an approximation to an inverse quadratic term becomes applicable. Conditions for computing stationary energies, as well as for establishing boundedness and normalizability of our solutions are discussed.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Few-Body Systems 物理-物理：综合

CiteScore

2.90

自引率

18.80%

发文量

审稿时长

6-12 weeks

期刊介绍： The journal Few-Body Systems presents original research work – experimental, theoretical and computational – investigating the behavior of any classical or quantum system consisting of a small number of well-defined constituent structures. The focus is on the research methods, properties, and results characteristic of few-body systems. Examples of few-body systems range from few-quark states, light nuclear and hadronic systems; few-electron atomic systems and small molecules; and specific systems in condensed matter and surface physics (such as quantum dots and highly correlated trapped systems), up to and including large-scale celestial structures. Systems for which an equivalent one-body description is available or can be designed, and large systems for which specific many-body methods are needed are outside the scope of the journal. The journal is devoted to the publication of all aspects of few-body systems research and applications. While concentrating on few-body systems well-suited to rigorous solutions, the journal also encourages interdisciplinary contributions that foster common approaches and insights, introduce and benchmark the use of novel tools (e.g. machine learning) and develop relevant applications (e.g. few-body aspects in quantum technologies).