梯度还原运动方程耦合簇三元组:计算电子激发能量的准确而经济的方法
IF 5.5
1区 化学
Q2 CHEMISTRY, PHYSICAL
引用次数: 0
摘要
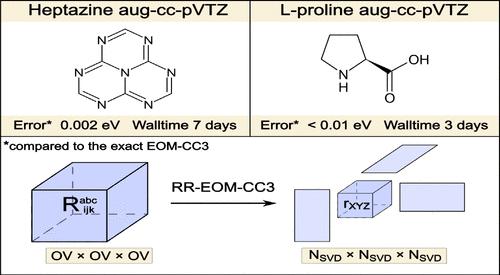
在本研究中,我们报告了带近似三重激发(RR-EOM-CC3)的秩缩减运动方程耦合簇方法的实现。所提出的变体依赖于张量分解技术,以减轻计算和处理三重激发振幅的高成本。在 RR-EOM-CC3 方法中,基态和激发态三重激发振幅都按照 Tucker-3 格式进行压缩。这样就能对工作方程进行因式分解,从而将该方法的形式缩放缩小到 N6,其中 N 为系统大小。我们方法的另一个优点是,可以通过适当选择两个参数来严格控制精确度,这两个参数定义了塔克分解法中基态和激发态的三重激发子空间的大小。本文讨论了选择这些参数的最佳策略。所开发的方法在一系列电子激发能量计算中进行了测试,并与经典的 EOM-CC3 方法进行了比较。与 FCI 相比,其误差比标准 EOM-CC3 方法的固有误差小数倍,这是可以直接实现的。这一结论既适用于以单激发为主的价态,也适用于具有明显双激发特性的价态。利用缩放比例降低的优势,我们展示了两个大分子--l-脯氨酸和庚嗪--计算成本的大幅降低(与标准 EOM-CC3 相比)。这说明了 RR-EOM-CC3 方法在精确测定大分子激发能量方面的实用性。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Rank-Reduced Equation-of-Motion Coupled Cluster Triples: an Accurate and Affordable Way of Calculating Electronic Excitation Energies
In the present work, we report an implementation of the rank-reduced equation-of-motion coupled cluster method with approximate triple excitations (RR-EOM-CC3). The proposed variant relies on tensor decomposition techniques in order to alleviate the high cost of computing and manipulating the triply excited amplitudes. In the RR-EOM-CC3 method, both ground-state and excited-state triple-excitation amplitudes are compressed according to the Tucker-3 format. This enables factorization of the working equations such that the formal scaling of the method is reduced to N6, where N is the system size. An additional advantage of our method is the fact that the accuracy can be strictly controlled by proper choice of two parameters defining sizes of triple-excitation subspaces in the Tucker decomposition for the ground and excited states. Optimal strategies of selecting these parameters are discussed. The developed method has been tested in a series of calculations of electronic excitation energies and compared to its canonical EOM-CC3 counterpart. Errors several times smaller than the inherent error of the canonical EOM-CC3 method (in comparison to FCI) are straightforward to achieve. This conclusion holds both for valence states dominated by single excitations and for states with pronounced doubly excited character. Taking advantage of the decreased scaling, we demonstrate substantial computational costs reductions (in comparison with the canonical EOM-CC3) in the case of two large molecules – l-proline and heptazine. This illustrates the usefulness of the RR-EOM-CC3 method for accurate determination of excitation energies of large molecules.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Journal of Chemical Theory and Computation
化学-物理:原子、分子和化学物理
CiteScore
9.90
自引率
16.40%
发文量
568
审稿时长
1 months
期刊介绍:
The Journal of Chemical Theory and Computation invites new and original contributions with the understanding that, if accepted, they will not be published elsewhere. Papers reporting new theories, methodology, and/or important applications in quantum electronic structure, molecular dynamics, and statistical mechanics are appropriate for submission to this Journal. Specific topics include advances in or applications of ab initio quantum mechanics, density functional theory, design and properties of new materials, surface science, Monte Carlo simulations, solvation models, QM/MM calculations, biomolecular structure prediction, and molecular dynamics in the broadest sense including gas-phase dynamics, ab initio dynamics, biomolecular dynamics, and protein folding. The Journal does not consider papers that are straightforward applications of known methods including DFT and molecular dynamics. The Journal favors submissions that include advances in theory or methodology with applications to compelling problems.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


