基于离散微分几何的轴对称壳体非线性分析模型
IF 7.1
1区 工程技术
Q1 ENGINEERING, MECHANICAL
International Journal of Mechanical Sciences
Pub Date : 2024-09-21
DOI:10.1016/j.ijmecsci.2024.109742
引用次数: 0
摘要
本文提出了一种基于离散微分几何(DDG)的新型一维(1D)数值方法,用于轴对称壳体结构的几何非线性力学分析(如屈曲和折断)。我们的数值模型利用微分几何原理准确捕捉轴对称壳体表现出的复杂非线性变形模式。通过将轴对称壳体沿经线方向离散为相互连接的一维元素,根据基尔霍夫-洛夫假设下一维节点和边缘的几何原理,制定了平面内拉伸和外弯曲势能,随后根据符号计算推导出运动方程所需的弹性力矢量和相关赫塞斯矩阵。通过与现有理论解法和文献中的有限元法(FEM)模拟进行广泛验证,我们的模型在预测轴对称壳体的非线性行为方面表现出很高的准确性。重要的是,与经典理论模型和三维(3D)有限元模拟相比,我们的模型具有很高的计算效率,因此适用于大规模实时模拟壳体结构的非线性问题,如失稳和快穿现象。此外,我们的框架还能轻松纳入复杂的加载条件,如边界非线性接触和多物理场驱动,这在软机器人和柔性设备等工程应用中发挥着至关重要的作用。这项研究表明,基于一维离散微分几何的方法既简单又有效,是对轴对称壳体非线性力学分析感兴趣的工程师和研究人员的有力工具,有望应用于各个工程领域。本文章由计算机程序翻译,如有差异,请以英文原文为准。
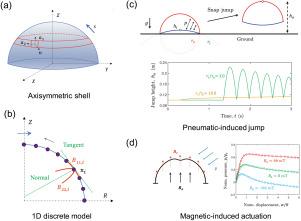
Discrete differential geometry-based model for nonlinear analysis of axisymmetric shells
In this paper, we propose a novel one-dimensional (1D) discrete differential geometry (DDG)-based numerical method for geometrically nonlinear mechanics analysis (e.g., buckling and snapping) of axisymmetric shell structures. Our numerical model leverages differential geometry principles to accurately capture the complex nonlinear deformation patterns exhibited by axisymmetric shells. By discretizing the axisymmetric shell into interconnected 1D elements along the meridional direction, the in-plane stretching and out-of-bending potentials are formulated based on the geometric principles of 1D nodes and edges under the Kirchhoff–Love hypothesis, and elastic force vector and associated Hessian matrix required by equations of motion are later derived based on symbolic calculation. Through extensive validation with available theoretical solutions and finite element method (FEM) simulations in literature, our model demonstrates high accuracy in predicting the nonlinear behavior of axisymmetric shells. Importantly, compared to the classical theoretical model and three-dimensional (3D) FEM simulation, our model is highly computationally efficient, making it suitable for large-scale real-time simulations of nonlinear problems of shell structures such as instability and snap-through phenomena. Moreover, our framework can easily incorporate complex loading conditions, e.g., boundary nonlinear contact and multi-physics actuation, which play an essential role in the use of engineering applications, such as soft robots and flexible devices. This study demonstrates that the simplicity and effectiveness of the 1D discrete differential geometry-based approach render it a powerful tool for engineers and researchers interested in nonlinear mechanics analysis of axisymmetric shells, with potential applications in various engineering fields.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

International Journal of Mechanical Sciences
工程技术-工程:机械
CiteScore
12.80
自引率
17.80%
发文量
769
审稿时长
19 days
期刊介绍:
The International Journal of Mechanical Sciences (IJMS) serves as a global platform for the publication and dissemination of original research that contributes to a deeper scientific understanding of the fundamental disciplines within mechanical, civil, and material engineering.
The primary focus of IJMS is to showcase innovative and ground-breaking work that utilizes analytical and computational modeling techniques, such as Finite Element Method (FEM), Boundary Element Method (BEM), and mesh-free methods, among others. These modeling methods are applied to diverse fields including rigid-body mechanics (e.g., dynamics, vibration, stability), structural mechanics, metal forming, advanced materials (e.g., metals, composites, cellular, smart) behavior and applications, impact mechanics, strain localization, and other nonlinear effects (e.g., large deflections, plasticity, fracture).
Additionally, IJMS covers the realms of fluid mechanics (both external and internal flows), tribology, thermodynamics, and materials processing. These subjects collectively form the core of the journal's content.
In summary, IJMS provides a prestigious platform for researchers to present their original contributions, shedding light on analytical and computational modeling methods in various areas of mechanical engineering, as well as exploring the behavior and application of advanced materials, fluid mechanics, thermodynamics, and materials processing.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


