局部导航规则对多路马尔可夫链中偏向随机游走的影响
IF 2.8
3区 物理与天体物理
Q2 PHYSICS, MULTIDISCIPLINARY
Physica A: Statistical Mechanics and its Applications
Pub Date : 2024-09-24
DOI:10.1016/j.physa.2024.130122
引用次数: 0
摘要
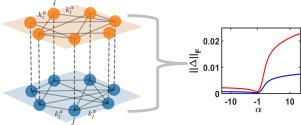
我们的研究重点是评估多路马尔可夫链(MMC)模型中偏置参数(α)的重要性,该模型的特点是多路网络中的偏置随机行走。我们探讨了不同的复杂网络拓扑结构如何影响作为偏置参数函数的总复用不平衡。我们的主要发现是,在偏置参数的正负两个区域内,系统的总不平衡度都会逐渐增加,在 α=-1 时出现一致的最小值。与负值区域相反,当 α 显著为正值时,总失衡度一直很高。我们对四种不同的网络结构进行了详细研究,并建立了三组多路复用网络。在每一组网络中,第二层都由常规随机网络组成,而第一层则是巴拉巴西-阿尔伯特网络、厄尔多斯-雷尼网络或瓦特-斯特罗加茨网络,具体取决于哪一组网络。我们的结果表明,Barabási-Albert 和随机正则网络的组合表现出最高水平的右饱和不平衡。此外,就左侧饱和不平衡而言,厄尔多斯-雷尼网络和随机正则网络的组合达到了稍高的值。我们还观察到,随着各层网络规模的增加,α=-1 时的不平衡总量呈下降趋势。此外,我们还能说明,超过渡矩阵的第二个最重要特征值对偏置参数变化的响应也呈现出类似的模式,与整个系统的不平衡性相一致。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Impact of local navigation rules on biased random walks in multiplex Markov chains
Our investigation centres on assessing the importance of a biased parameter () in a multiplex Markov chain (MMC) model that is characterized by biased random walks in multiplex networks. We explore how varying complex network topologies affect the total multiplex imbalance as a function of biased parameter. Our primary finding is that the system demonstrates a gradual increase in total imbalance within both positive and negative regions of the biased parameter, with a consistent minimum value occurring at . In contrast to the negative region, the total imbalance is consistently high when is significantly positive. We perform a detailed examination of four different network structures and establish three sets of multiplex networks. In each of these networks, the second layer consists of a Regular Random network, while the first layer is either a Barabási–Albert, Erdős-Rényi, or Watts Strogatz network, depending on the set. Our results demonstrate that the combination of Barabási–Albert and Random Regular Network exhibits the highest level of right saturation imbalance. Additionally, for left saturation imbalance, the Erdős–Rényi and Random Regular combination achieve a slightly higher value. We also observe that the total amount of imbalance at follows a decreasing trend as the size of the network of each layer increases. Furthermore, we are also able to illustrate that the second most significant eigenvalue of the supra-transition matrix exhibits a similar pattern in response to changes in the bias parameter, aligning with the overall system’s imbalance.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
7.20
自引率
9.10%
发文量
852
审稿时长
6.6 months
期刊介绍:
Physica A: Statistical Mechanics and its Applications
Recognized by the European Physical Society
Physica A publishes research in the field of statistical mechanics and its applications.
Statistical mechanics sets out to explain the behaviour of macroscopic systems by studying the statistical properties of their microscopic constituents.
Applications of the techniques of statistical mechanics are widespread, and include: applications to physical systems such as solids, liquids and gases; applications to chemical and biological systems (colloids, interfaces, complex fluids, polymers and biopolymers, cell physics); and other interdisciplinary applications to for instance biological, economical and sociological systems.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


