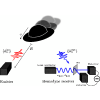
Heisenberg-Limited Quantum Lidar for Joint Range and Velocity Estimation

We propose a quantum lidar protocol to jointly estimate the range and velocity of a target by illuminating it with a single beam of pulsed displaced squeezed light. In the lossless scenario, we show that the mean-squared errors of both range and velocity estimations are inversely proportional to the squared number of signal photons, simultaneously attaining the Heisenberg limit. This is achieved by engineering the multiphoton squeezed state of the temporal modes and adopting standard homodyne detection. To assess the robustness of the quantum protocol, we incorporate photon losses and detuning of the homodyne receiver. Our findings reveal a quantum advantage over the best-known classical strategy across a wide range of round-trip transmissivities. Particularly, the quantum advantage is substantial for sufficiently small losses, even when compared to the optimal—potentially unattainable—classical performance limit. The quantum advantage also extends to the practical case where quantum engineering is done on top of a strong classical coherent state with watts of power. This, together with the robustness against losses and the feasibility of the measurement with state-of-the-art technology, make the protocol highly promising for near-term implementation.