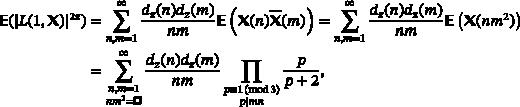
Asymmetric distribution of extreme values of cubic L $L$ -functions at s = 1 $s=1$

We investigate the distribution of values of cubic Dirichlet $L$-functions at $s=1$. Following ideas of Granville and Soundararajan for quadratic $L$-functions, we model the distribution of $L(1,\chi )$ by the distribution of random Euler products $L(1,X)$ for certain family of random variables $X\left(p\right)$ attached to each prime. We obtain a description of the proportion of $\left|L\right(1,\chi \left)\right|$ that is larger or that is smaller than a given bound, and yield more light into the Littlewood bounds. Unlike the quadratic case, there is an asymmetry between lower and upper bounds for the cubic case, and small values are less probable than large values.