带有三角函数障碍的无限方井的格罗斯-皮塔耶夫斯基方程

IF 1.1 3区物理与天体物理 Q4 PHYSICS, APPLIED

Journal of Low Temperature Physics Pub Date : 2024-08-23 DOI:10.1007/s10909-024-03195-x

Robert J. Ragan, Asaad R. Sakhel, William J. Mullin

{"title":"带有三角函数障碍的无限方井的格罗斯-皮塔耶夫斯基方程","authors":"Robert J. Ragan, Asaad R. Sakhel, William J. Mullin","doi":"10.1007/s10909-024-03195-x","DOIUrl":null,"url":null,"abstract":"<div><p>The Gross–Pitaevskii equation is solved by analytic methods for an external double-well potential, that is, an infinite square well plus a <span>\\(\\delta\\)</span>-function central barrier. We find solutions that have the symmetry of the non-interacting Hamiltonian as well as asymmetric solutions that bifurcate from the symmetric solutions for attractive interactions and from the antisymmetric solutions for repulsive interactions. We present a variational approximation to the asymmetric state as well as an approximate numerical approach. We compare with other approximate methods. Stability of the states is considered.</p></div>","PeriodicalId":641,"journal":{"name":"Journal of Low Temperature Physics","volume":"216 5-6","pages":"814 - 838"},"PeriodicalIF":1.1000,"publicationDate":"2024-08-23","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"The Gross–Pitaevskii Equation for an Infinite Square Well with a Delta-Function Barrier\",\"authors\":\"Robert J. Ragan, Asaad R. Sakhel, William J. Mullin\",\"doi\":\"10.1007/s10909-024-03195-x\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>The Gross–Pitaevskii equation is solved by analytic methods for an external double-well potential, that is, an infinite square well plus a <span>\\\\(\\\\delta\\\\)</span>-function central barrier. We find solutions that have the symmetry of the non-interacting Hamiltonian as well as asymmetric solutions that bifurcate from the symmetric solutions for attractive interactions and from the antisymmetric solutions for repulsive interactions. We present a variational approximation to the asymmetric state as well as an approximate numerical approach. We compare with other approximate methods. Stability of the states is considered.</p></div>\",\"PeriodicalId\":641,\"journal\":{\"name\":\"Journal of Low Temperature Physics\",\"volume\":\"216 5-6\",\"pages\":\"814 - 838\"},\"PeriodicalIF\":1.1000,\"publicationDate\":\"2024-08-23\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Low Temperature Physics\",\"FirstCategoryId\":\"101\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s10909-024-03195-x\",\"RegionNum\":3,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"PHYSICS, APPLIED\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Low Temperature Physics","FirstCategoryId":"101","ListUrlMain":"https://link.springer.com/article/10.1007/s10909-024-03195-x","RegionNum":3,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"PHYSICS, APPLIED","Score":null,"Total":0}

引用次数: 0

摘要

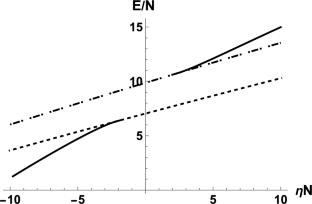
格罗斯-皮塔耶夫斯基方程是通过对外部双阱势，即一个无限方阱加上一个（\△）函数中心壁垒的解析方法求解的。我们发现了具有非相互作用哈密顿对称性的解，以及从对称解分岔出吸引力相互作用和从非对称解分岔出排斥力相互作用的非对称解。我们提出了非对称状态的变分近似以及近似数值方法。我们与其他近似方法进行了比较。我们还考虑了状态的稳定性。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

The Gross–Pitaevskii Equation for an Infinite Square Well with a Delta-Function Barrier

查看原文本刊更多论文

The Gross–Pitaevskii Equation for an Infinite Square Well with a Delta-Function Barrier

The Gross–Pitaevskii equation is solved by analytic methods for an external double-well potential, that is, an infinite square well plus a \(\delta\)-function central barrier. We find solutions that have the symmetry of the non-interacting Hamiltonian as well as asymmetric solutions that bifurcate from the symmetric solutions for attractive interactions and from the antisymmetric solutions for repulsive interactions. We present a variational approximation to the asymmetric state as well as an approximate numerical approach. We compare with other approximate methods. Stability of the states is considered.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Low Temperature Physics 物理-物理：凝聚态物理

CiteScore

3.30

自引率

25.00%

发文量

245

审稿时长

1 months

期刊介绍： The Journal of Low Temperature Physics publishes original papers and review articles on all areas of low temperature physics and cryogenics, including theoretical and experimental contributions. Subject areas include: Quantum solids, liquids and gases; Superfluidity; Superconductivity; Condensed matter physics; Experimental techniques; The Journal encourages the submission of Rapid Communications and Special Issues.