工作波动总和规则

IF 2.4 3区物理与天体物理 Q1 Mathematics

Physical review. E Pub Date : 2024-09-03 DOI:10.1103/physreve.110.034108

Hyogeon Park, Yong Woon Kim, Juyeon Yi

{"title":"工作波动总和规则","authors":"Hyogeon Park, Yong Woon Kim, Juyeon Yi","doi":"10.1103/physreve.110.034108","DOIUrl":null,"url":null,"abstract":"We study the fluctuations of work caused by applying cyclic perturbations and obtain an exact sum rule satisfied by the moments of work for a broad class of quantum stationary ensembles. In the case of the canonical ensemble, the sum rule reproduces the Jarzynski equality. The sum rule can also be simplified into a linear relationship between the work average and the second moment of work, which we numerically confirm via an exact diagonalization of a spin model system.","PeriodicalId":20085,"journal":{"name":"Physical review. E","volume":"17 1","pages":""},"PeriodicalIF":2.4000,"publicationDate":"2024-09-03","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Sum rule for fluctuations of work\",\"authors\":\"Hyogeon Park, Yong Woon Kim, Juyeon Yi\",\"doi\":\"10.1103/physreve.110.034108\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"We study the fluctuations of work caused by applying cyclic perturbations and obtain an exact sum rule satisfied by the moments of work for a broad class of quantum stationary ensembles. In the case of the canonical ensemble, the sum rule reproduces the Jarzynski equality. The sum rule can also be simplified into a linear relationship between the work average and the second moment of work, which we numerically confirm via an exact diagonalization of a spin model system.\",\"PeriodicalId\":20085,\"journal\":{\"name\":\"Physical review. E\",\"volume\":\"17 1\",\"pages\":\"\"},\"PeriodicalIF\":2.4000,\"publicationDate\":\"2024-09-03\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Physical review. E\",\"FirstCategoryId\":\"101\",\"ListUrlMain\":\"https://doi.org/10.1103/physreve.110.034108\",\"RegionNum\":3,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"Mathematics\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Physical review. E","FirstCategoryId":"101","ListUrlMain":"https://doi.org/10.1103/physreve.110.034108","RegionNum":3,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"Mathematics","Score":null,"Total":0}

引用次数: 0

摘要

我们研究了周期性扰动引起的功的波动，并获得了一大类量子静态集合功矩满足的精确总和规则。在典型集合的情况下，和规则再现了 Jarzynski 等式。我们通过自旋模型系统的精确对角化，从数值上证实了这一点。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

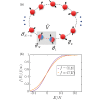
Sum rule for fluctuations of work

查看原文本刊更多论文

Sum rule for fluctuations of work

We study the fluctuations of work caused by applying cyclic perturbations and obtain an exact sum rule satisfied by the moments of work for a broad class of quantum stationary ensembles. In the case of the canonical ensemble, the sum rule reproduces the Jarzynski equality. The sum rule can also be simplified into a linear relationship between the work average and the second moment of work, which we numerically confirm via an exact diagonalization of a spin model system.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Physical review. E 物理-物理：流体与等离子体

CiteScore

4.60

自引率

16.70%

发文量

审稿时长

3.3 months

期刊介绍： Physical Review E (PRE), broad and interdisciplinary in scope, focuses on collective phenomena of many-body systems, with statistical physics and nonlinear dynamics as the central themes of the journal. Physical Review E publishes recent developments in biological and soft matter physics including granular materials, colloids, complex fluids, liquid crystals, and polymers. The journal covers fluid dynamics and plasma physics and includes sections on computational and interdisciplinary physics, for example, complex networks.