二方信息热动力系统的效率边界

IF 2.4 3区物理与天体物理 Q1 Mathematics

Physical review. E Pub Date : 2024-09-03 DOI:10.1103/physreve.110.034102

Shihao Xia, Shuanglong Han, Ousi Pan, Yuzhuo Pan, Jincan Chen, Shanhe Su

{"title":"二方信息热动力系统的效率边界","authors":"Shihao Xia, Shuanglong Han, Ousi Pan, Yuzhuo Pan, Jincan Chen, Shanhe Su","doi":"10.1103/physreve.110.034102","DOIUrl":null,"url":null,"abstract":"In this paper, we introduce an approach to derive a lower bound for the entropy production rate of a subsystem by utilizing the Cauchy-Schwarz inequality. It extends to establishing comprehensive upper and lower bounds for the efficiency of two subsystems. These bounds are applicable to a wide range of Markovian stochastic processes, which enhances the accuracy in depicting the range of energy conversion efficiency between subsystems. Empirical validation is conducted using a two-quantum-dot system model, which serves to confirm the effectiveness of our inequality in refining the boundaries of efficiency.","PeriodicalId":20085,"journal":{"name":"Physical review. E","volume":"1 1","pages":""},"PeriodicalIF":2.4000,"publicationDate":"2024-09-03","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Efficiency bounds for bipartite information-thermodynamic systems\",\"authors\":\"Shihao Xia, Shuanglong Han, Ousi Pan, Yuzhuo Pan, Jincan Chen, Shanhe Su\",\"doi\":\"10.1103/physreve.110.034102\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"In this paper, we introduce an approach to derive a lower bound for the entropy production rate of a subsystem by utilizing the Cauchy-Schwarz inequality. It extends to establishing comprehensive upper and lower bounds for the efficiency of two subsystems. These bounds are applicable to a wide range of Markovian stochastic processes, which enhances the accuracy in depicting the range of energy conversion efficiency between subsystems. Empirical validation is conducted using a two-quantum-dot system model, which serves to confirm the effectiveness of our inequality in refining the boundaries of efficiency.\",\"PeriodicalId\":20085,\"journal\":{\"name\":\"Physical review. E\",\"volume\":\"1 1\",\"pages\":\"\"},\"PeriodicalIF\":2.4000,\"publicationDate\":\"2024-09-03\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Physical review. E\",\"FirstCategoryId\":\"101\",\"ListUrlMain\":\"https://doi.org/10.1103/physreve.110.034102\",\"RegionNum\":3,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"Mathematics\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Physical review. E","FirstCategoryId":"101","ListUrlMain":"https://doi.org/10.1103/physreve.110.034102","RegionNum":3,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"Mathematics","Score":null,"Total":0}

引用次数: 0

摘要

本文介绍了一种利用考希-施瓦茨不等式推导子系统熵产生率下限的方法。它扩展到为两个子系统的效率建立全面的上界和下界。这些界限适用于多种马尔可夫随机过程，从而提高了描述子系统间能量转换效率范围的准确性。我们使用双量子点系统模型进行了经验验证，证实了我们的不等式在完善效率边界方面的有效性。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

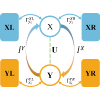
Efficiency bounds for bipartite information-thermodynamic systems

查看原文本刊更多论文

Efficiency bounds for bipartite information-thermodynamic systems

In this paper, we introduce an approach to derive a lower bound for the entropy production rate of a subsystem by utilizing the Cauchy-Schwarz inequality. It extends to establishing comprehensive upper and lower bounds for the efficiency of two subsystems. These bounds are applicable to a wide range of Markovian stochastic processes, which enhances the accuracy in depicting the range of energy conversion efficiency between subsystems. Empirical validation is conducted using a two-quantum-dot system model, which serves to confirm the effectiveness of our inequality in refining the boundaries of efficiency.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Physical review. E 物理-物理：流体与等离子体

CiteScore

4.60

自引率

16.70%

发文量

审稿时长

3.3 months

期刊介绍： Physical Review E (PRE), broad and interdisciplinary in scope, focuses on collective phenomena of many-body systems, with statistical physics and nonlinear dynamics as the central themes of the journal. Physical Review E publishes recent developments in biological and soft matter physics including granular materials, colloids, complex fluids, liquid crystals, and polymers. The journal covers fluid dynamics and plasma physics and includes sections on computational and interdisciplinary physics, for example, complex networks.