关于具有唯一哈密顿循环的顶点变换图

IF 0.9 3区数学 Q2 MATHEMATICS

Journal of Graph Theory Pub Date : 2024-08-22 DOI:10.1002/jgt.23166

Babak Miraftab, Dave Witte Morris

{"title":"关于具有唯一哈密顿循环的顶点变换图","authors":"Babak Miraftab, Dave Witte Morris","doi":"10.1002/jgt.23166","DOIUrl":null,"url":null,"abstract":"A graph is said to be uniquely hamiltonian if it has a unique hamiltonian cycle. For a natural extension of this concept to infinite graphs, we find all uniquely hamiltonian vertex-transitive graphs with finitely many ends, and also discuss some examples with infinitely many ends. In particular, we show each nonabelian free group <math>\n \n <mrow>\n <msub>\n <mi>F</mi>\n \n <mi>n</mi>\n </msub>\n </mrow></math> has a Cayley graph of degree <math>\n \n <mrow>\n <mn>2</mn>\n \n <mi>n</mi>\n \n <mo>+</mo>\n \n <mn>2</mn>\n </mrow></math> that has a unique hamiltonian circle. (A weaker statement had been conjectured by Georgakopoulos.) Furthermore, we prove that these Cayley graphs of <math>\n \n <mrow>\n <msub>\n <mi>F</mi>\n \n <mi>n</mi>\n </msub>\n </mrow></math> are outerplanar.","PeriodicalId":16014,"journal":{"name":"Journal of Graph Theory","volume":"108 1","pages":"65-99"},"PeriodicalIF":0.9000,"publicationDate":"2024-08-22","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1002/jgt.23166","citationCount":"0","resultStr":"{\"title\":\"On vertex-transitive graphs with a unique hamiltonian cycle\",\"authors\":\"Babak Miraftab, Dave Witte Morris\",\"doi\":\"10.1002/jgt.23166\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"A graph is said to be uniquely hamiltonian if it has a unique hamiltonian cycle. For a natural extension of this concept to infinite graphs, we find all uniquely hamiltonian vertex-transitive graphs with finitely many ends, and also discuss some examples with infinitely many ends. In particular, we show each nonabelian free group <math>\\n \\n <mrow>\\n <msub>\\n <mi>F</mi>\\n \\n <mi>n</mi>\\n </msub>\\n </mrow></math> has a Cayley graph of degree <math>\\n \\n <mrow>\\n <mn>2</mn>\\n \\n <mi>n</mi>\\n \\n <mo>+</mo>\\n \\n <mn>2</mn>\\n </mrow></math> that has a unique hamiltonian circle. (A weaker statement had been conjectured by Georgakopoulos.) Furthermore, we prove that these Cayley graphs of <math>\\n \\n <mrow>\\n <msub>\\n <mi>F</mi>\\n \\n <mi>n</mi>\\n </msub>\\n </mrow></math> are outerplanar.\",\"PeriodicalId\":16014,\"journal\":{\"name\":\"Journal of Graph Theory\",\"volume\":\"108 1\",\"pages\":\"65-99\"},\"PeriodicalIF\":0.9000,\"publicationDate\":\"2024-08-22\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1002/jgt.23166\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Graph Theory\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1002/jgt.23166\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Graph Theory","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1002/jgt.23166","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

如果一个图具有唯一的哈密顿循环，那么这个图就是唯一哈密顿图。为了将这一概念自然扩展到无限图，我们找到了所有具有有限多个末端的唯一哈密顿顶点传递图，并讨论了一些具有无限多个末端的例子。特别是，我们证明了每个非阿贝尔自由群都有一个具有唯一哈密顿圆的阶数 Cayley 图。(此外，我们还证明了这些 Cayley 图是外平面的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

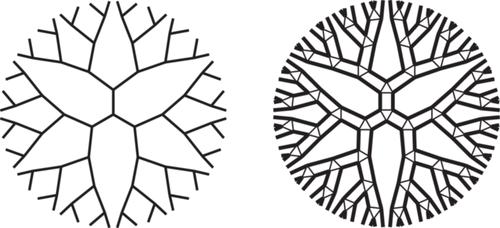
On vertex-transitive graphs with a unique hamiltonian cycle

查看原文本刊更多论文

On vertex-transitive graphs with a unique hamiltonian cycle

A graph is said to be uniquely hamiltonian if it has a unique hamiltonian cycle. For a natural extension of this concept to infinite graphs, we find all uniquely hamiltonian vertex-transitive graphs with finitely many ends, and also discuss some examples with infinitely many ends. In particular, we show each nonabelian free group $F_{n}$ has a Cayley graph of degree $2 n + 2$ that has a unique hamiltonian circle. (A weaker statement had been conjectured by Georgakopoulos.) Furthermore, we prove that these Cayley graphs of $F_{n}$ are outerplanar.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Graph Theory 数学-数学

CiteScore

1.60

自引率

22.20%

发文量

130

审稿时长

6-12 weeks

期刊介绍： The Journal of Graph Theory is devoted to a variety of topics in graph theory, such as structural results about graphs, graph algorithms with theoretical emphasis, and discrete optimization on graphs. The scope of the journal also includes related areas in combinatorics and the interaction of graph theory with other mathematical sciences. A subscription to the Journal of Graph Theory includes a subscription to the Journal of Combinatorial Designs .