动感参数转换器
IF 4.4
2区 物理与天体物理
Q2 PHYSICS, APPLIED
引用次数: 0
摘要
参量转换器是一种参量放大器,它混合了两个空间上独立的非退行模式,通常用于放大和挤压量子计算和传感中的微波信号。在约瑟夫森参数转换器中,约瑟夫森结的强局部非线性限制了当前设备的放大和挤压以及动态范围。与此相反,弱分布式非线性可以提供更高的增益和动态范围,当作为脏超导体的动电感(KI)纳米线实现时,还具有抗磁场、更高温度操作和简化制造等额外优势。在此,我们提出、演示并分析了一种 KI 参数转换器的性能,该转换器依赖于 Nb-Ti-N KI 纳米线的微弱分布式非线性。该器件利用直流电流偏压诱导的三波混合。我们展示了它作为具有高相位敏感增益的非衰减参量放大器的运行情况,在两个相隔 0.8 GHz 的谐振中,它的双模放大和去放大率约为 30 dB,与我们的器件理论非常吻合。我们观察到 30 dB 增益时的动态范围为 -108 dBm。我们的器件可以大大拓宽量子限幅信号处理器件的应用范围,包括保相放大和双模挤压。本文章由计算机程序翻译,如有差异,请以英文原文为准。
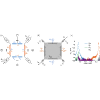
Kinetic inductance parametric converter
Parametric converters are parametric amplifiers that mix two spatially separate nondegenerate modes and are commonly used for amplifying and squeezing microwave signals in quantum computing and sensing. In Josephson parametric converters, the strong localized nonlinearity of the Josephson junction limits the amplification and squeezing, as well as the dynamic range, in current devices. In contrast, a weak distributed nonlinearity can provide higher gain and dynamic range, when implemented as a kinetic inductance (KI) nanowire of a dirty superconductor, and has additional benefits such as resilience to magnetic field, higher-temperature operation, and simplified fabrication. Here, we propose, demonstrate, and analyze the performance of a KI parametric converter that relies on the weak distributed nonlinearity of a Nb-Ti-N KI nanowire. The device utilizes three-wave mixing induced by a dc current bias. We demonstrate its operation as a nondegenerate parametric amplifier with high phase-sensitive gain, reaching two-mode amplification and deamplification of approximately 30 dB for two resonances separated by 0.8 GHz, in excellent agreement with our theory of the device. We observe a dynamic range of dBm at 30 dB gain. Our device can significantly broaden applications of quantum-limited signal processing devices including phase-preserving amplification and two-mode squeezing.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Physical Review Applied
PHYSICS, APPLIED-
CiteScore
7.80
自引率
8.70%
发文量
760
审稿时长
2.5 months
期刊介绍:
Physical Review Applied (PRApplied) publishes high-quality papers that bridge the gap between engineering and physics, and between current and future technologies. PRApplied welcomes papers from both the engineering and physics communities, in academia and industry.
PRApplied focuses on topics including:
Biophysics, bioelectronics, and biomedical engineering,
Device physics,
Electronics,
Technology to harvest, store, and transmit energy, focusing on renewable energy technologies,
Geophysics and space science,
Industrial physics,
Magnetism and spintronics,
Metamaterials,
Microfluidics,
Nonlinear dynamics and pattern formation in natural or manufactured systems,
Nanoscience and nanotechnology,
Optics, optoelectronics, photonics, and photonic devices,
Quantum information processing, both algorithms and hardware,
Soft matter physics, including granular and complex fluids and active matter.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


