来自有限温度易平面磁性的可扩展自旋挤压
IF 17.6
1区 物理与天体物理
Q1 PHYSICS, MULTIDISCIPLINARY
引用次数: 0
摘要
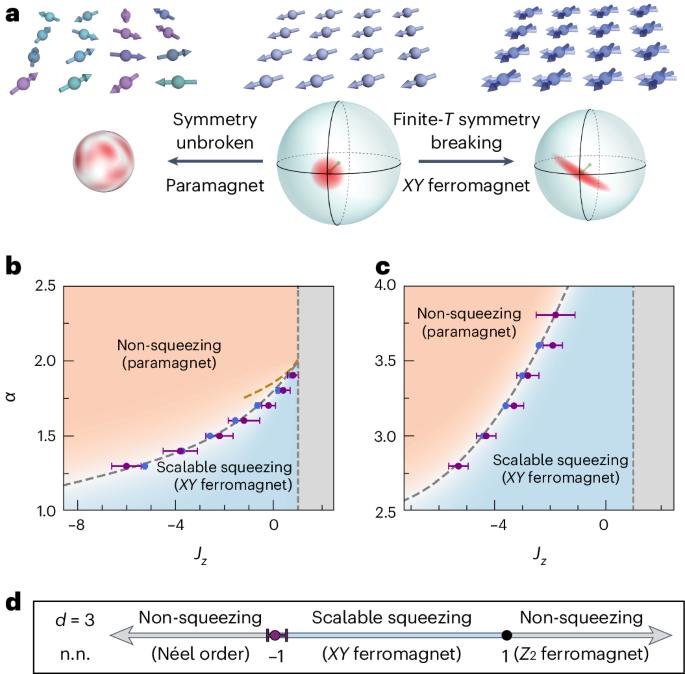
自旋挤压是一种重塑量子投影噪声以提高测量精度的纠缠形式。在这里,我们为以下猜想提供了数值和分析证据:任何表现出有限温度易平面铁磁性的哈密顿都可以用来产生可扩展的自旋挤压,从而实现量子增强传感。我们的猜想以纯态的量子费雪信息与连续对称性的自发破缺之间的联系为指导。我们证明,自旋挤压呈现出一个相图,在可扩展挤压和非挤压之间有一个尖锐的过渡。这一转变与有限温度下 XY 阶的平衡相边界相吻合。在可伸缩挤压阶段,我们预测灵敏度缩放介于标准量子极限和全对全耦合单轴扭转模型的缩放之间。我们猜想的一个推论是,双轴扭转的短程版本无法产生可扩展的计量增益。我们的研究结果让我们深入了解了可用于生成计量学上有用的量子态的哈密顿形式。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Scalable spin squeezing from finite-temperature easy-plane magnetism
Spin squeezing is a form of entanglement that reshapes the quantum projection noise to improve measurement precision. Here, we provide numerical and analytic evidence for the following conjecture: any Hamiltonian exhibiting finite-temperature easy-plane ferromagnetism can be used to generate scalable spin squeezing, thereby enabling quantum-enhanced sensing. Our conjecture is guided by a connection between the quantum Fisher information of pure states and the spontaneous breaking of a continuous symmetry. We demonstrate that spin squeezing exhibits a phase diagram with a sharp transition between scalable squeezing and non-squeezing. This transition coincides with the equilibrium phase boundary for XY order at a finite temperature. In the scalable squeezing phase, we predict a sensitivity scaling that lies between the standard quantum limit and the scaling achieved in all-to-all coupled one-axis twisting models. A corollary of our conjecture is that short-ranged versions of two-axis twisting cannot yield scalable metrological gain. Our results provide insights into the landscape of Hamiltonians that can be used to generate metrologically useful quantum states. Generating highly squeezed states for quantum sensing requires precise entanglement properties, which makes it a hard task. Now a conjecture identifies a realistic regime of magnetic order at finite temperatures that enables scalable spin squeezing.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Nature Physics
物理-物理:综合
CiteScore
30.40
自引率
2.00%
发文量
349
审稿时长
4-8 weeks
期刊介绍:
Nature Physics is dedicated to publishing top-tier original research in physics with a fair and rigorous review process. It provides high visibility and access to a broad readership, maintaining high standards in copy editing and production, ensuring rapid publication, and maintaining independence from academic societies and other vested interests.
The journal presents two main research paper formats: Letters and Articles. Alongside primary research, Nature Physics serves as a central source for valuable information within the physics community through Review Articles, News & Views, Research Highlights covering crucial developments across the physics literature, Commentaries, Book Reviews, and Correspondence.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


