用模糊（m，n）子结构描述有序半群的特征

IF 3.1 3区计算机科学 Q2 COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCE

Soft Computing Pub Date : 2024-07-26 DOI:10.1007/s00500-024-09880-z

Ahsan Mahboob, M. Al-Tahan, Ghulam Muhiuddin

引用次数: 0

摘要

本文从多个方面发展和讨论了有序半群中的模糊（m，n）准等式的概念。此外，我们还提出了有序半群中的模糊（m，0）准边和模糊（0，n）准边的概念，并研究了它们的一些相关性质。此外，我们还从模糊 (m, n) 准等边、模糊 (m, 0) 等边和模糊 (0, n) 等边的角度研究了 (m, n) 不规则有序半群。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

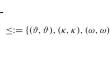
Characterizations of ordered semigroups in terms of fuzzy (m, n)-substructures

查看原文本刊更多论文

Characterizations of ordered semigroups in terms of fuzzy (m, n)-substructures

In this article, the concept of fuzzy (m, n)-quasi-ideals in ordered semigroups is developed and discussed in various ways. In addition, we present the concepts of fuzzy (m, 0)-ideals and fuzzy (0, n)-ideals in ordered semigroups and investigate some of their associated properties. Furthermore, the (m, n)-regular ordered semigroups are studied in terms of fuzzy (m, n)-quasi-ideals, fuzzy (m, 0)-ideals, and fuzzy (0, n)-ideals.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Soft Computing 工程技术-计算机：跨学科应用

CiteScore

8.10

自引率

9.80%

发文量

927

审稿时长

7.3 months

期刊介绍： Soft Computing is dedicated to system solutions based on soft computing techniques. It provides rapid dissemination of important results in soft computing technologies, a fusion of research in evolutionary algorithms and genetic programming, neural science and neural net systems, fuzzy set theory and fuzzy systems, and chaos theory and chaotic systems. Soft Computing encourages the integration of soft computing techniques and tools into both everyday and advanced applications. By linking the ideas and techniques of soft computing with other disciplines, the journal serves as a unifying platform that fosters comparisons, extensions, and new applications. As a result, the journal is an international forum for all scientists and engineers engaged in research and development in this fast growing field.