具有张量预因子的显相关高斯：解析矩阵元素

IF 1.7 4区物理与天体物理 Q2 PHYSICS, MULTIDISCIPLINARY

Few-Body Systems Pub Date : 2024-07-17 DOI:10.1007/s00601-024-01945-x

D. V. Fedorov, A. F. Teilmann, M. C. Østerlund, T. L. Norrbohm

{"title":"具有张量预因子的显相关高斯：解析矩阵元素","authors":"D. V. Fedorov, A. F. Teilmann, M. C. Østerlund, T. L. Norrbohm","doi":"10.1007/s00601-024-01945-x","DOIUrl":null,"url":null,"abstract":"<div><p>We consider a specific form of explicitly correlated Gaussians—with tensor pre-factors—which appear naturally when dealing with certain few-body systems in nuclear and particle physics. We derive analytic matrix elements with these Gaussians—overlap, kinetic energy, and Coulomb potential—to be used in variational calculations of those systems. We also perform a quick test of the derived formulae by applying them to p- and d-waves of the hydrogen atom.</p></div>","PeriodicalId":556,"journal":{"name":"Few-Body Systems","volume":null,"pages":null},"PeriodicalIF":1.7000,"publicationDate":"2024-07-17","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://link.springer.com/content/pdf/10.1007/s00601-024-01945-x.pdf","citationCount":"0","resultStr":"{\"title\":\"Explicitly Correlated Gaussians with Tensor Pre-factors: Analytic Matrix Elements\",\"authors\":\"D. V. Fedorov, A. F. Teilmann, M. C. Østerlund, T. L. Norrbohm\",\"doi\":\"10.1007/s00601-024-01945-x\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>We consider a specific form of explicitly correlated Gaussians—with tensor pre-factors—which appear naturally when dealing with certain few-body systems in nuclear and particle physics. We derive analytic matrix elements with these Gaussians—overlap, kinetic energy, and Coulomb potential—to be used in variational calculations of those systems. We also perform a quick test of the derived formulae by applying them to p- and d-waves of the hydrogen atom.</p></div>\",\"PeriodicalId\":556,\"journal\":{\"name\":\"Few-Body Systems\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":1.7000,\"publicationDate\":\"2024-07-17\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://link.springer.com/content/pdf/10.1007/s00601-024-01945-x.pdf\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Few-Body Systems\",\"FirstCategoryId\":\"101\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s00601-024-01945-x\",\"RegionNum\":4,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"PHYSICS, MULTIDISCIPLINARY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Few-Body Systems","FirstCategoryId":"101","ListUrlMain":"https://link.springer.com/article/10.1007/s00601-024-01945-x","RegionNum":4,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"PHYSICS, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

摘要

我们考虑了显式相关高斯的一种特定形式--带有张量预因子--这种高斯在处理核物理和粒子物理中的某些少体系统时自然出现。我们推导出这些高斯的解析矩阵元素--重叠、动能和库仑势--用于这些系统的变分计算。我们还将推导出的公式应用于氢原子的 p 波和 d 波，对其进行了快速测试。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

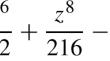
Explicitly Correlated Gaussians with Tensor Pre-factors: Analytic Matrix Elements

查看原文本刊更多论文

Explicitly Correlated Gaussians with Tensor Pre-factors: Analytic Matrix Elements

We consider a specific form of explicitly correlated Gaussians—with tensor pre-factors—which appear naturally when dealing with certain few-body systems in nuclear and particle physics. We derive analytic matrix elements with these Gaussians—overlap, kinetic energy, and Coulomb potential—to be used in variational calculations of those systems. We also perform a quick test of the derived formulae by applying them to p- and d-waves of the hydrogen atom.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Few-Body Systems 物理-物理：综合

CiteScore

2.90

自引率

18.80%

发文量

审稿时长

6-12 weeks

期刊介绍： The journal Few-Body Systems presents original research work – experimental, theoretical and computational – investigating the behavior of any classical or quantum system consisting of a small number of well-defined constituent structures. The focus is on the research methods, properties, and results characteristic of few-body systems. Examples of few-body systems range from few-quark states, light nuclear and hadronic systems; few-electron atomic systems and small molecules; and specific systems in condensed matter and surface physics (such as quantum dots and highly correlated trapped systems), up to and including large-scale celestial structures. Systems for which an equivalent one-body description is available or can be designed, and large systems for which specific many-body methods are needed are outside the scope of the journal. The journal is devoted to the publication of all aspects of few-body systems research and applications. While concentrating on few-body systems well-suited to rigorous solutions, the journal also encourages interdisciplinary contributions that foster common approaches and insights, introduce and benchmark the use of novel tools (e.g. machine learning) and develop relevant applications (e.g. few-body aspects in quantum technologies).