收缩比 λ=1 的二次吸引细分
IF 2.5
4区 计算机科学
Q2 COMPUTER SCIENCE, SOFTWARE ENGINEERING
引用次数: 0
摘要
经典的广义细分(如 Catmull-Clark 细分)以及最新的高质量曲面细分算法,都依赖于由 n>4 个四边形包围的网格节点向非常点的缓慢收敛。缓慢收敛相当于 λ>0.5 的收缩比。为了改善形状,防止参数化与表面生长不协调,或改善非常点附近等几何分析的收敛性,许多算法通过改变细化规则来明确调整 λ。然而,迄今为止,这种对 λ 的调整导致了较差的表面质量,表现为高亮线的不均匀分布或摆动。最近的二次吸引细分法(QAS)基于对中心点二次展开的谨慎选择,生成高质量、有约束曲率的曲面,并且与 Catmull-Clark 细分法一样,通过矩阵乘法创建下一个细分环的控制点。但当 n>4 时,QAS 与 Catmull-Clark 细分的收缩率 λCC>1/2 相同。当 n=5,...,10 时,与 QAS 相比,QAS+ 提高了对二元域细化的统一 λ=12 的收敛性,且不影响曲面质量。 本文章由计算机程序翻译,如有差异,请以英文原文为准。
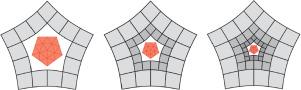
Quadratic-attraction subdivision with contraction-ratio λ=12
Classic generalized subdivision, such as Catmull–Clark subdivision, as well as recent subdivision algorithms for high-quality surfaces, rely on slower convergence towards extraordinary points for mesh nodes surrounded by quadrilaterals. Slow convergence corresponds to a contraction-ratio of . To improve shape, prevent parameterization discordant with surface growth, or to improve convergence in isogeometric analysis near extraordinary points, a number of algorithms explicitly adjust by altering refinement rules. However, such tuning of has so far led to poorer surface quality, visible as uneven distribution or oscillation of highlight lines. The recent Quadratic-Attraction Subdivision (QAS) generates high-quality, bounded curvature surfaces based on a careful choice of quadratic expansion at the central point and, just like Catmull–Clark subdivision, creates the control points of the next subdivision ring by matrix multiplication. But QAS shares the contraction-ratio of Catmull–Clark subdivision when . For , QAS improves the convergence to the uniform of binary domain refinement and without sacrificing surface quality compared to QAS.
摘要
经典的广义细分(如 Catmull-Clark 细分)以及最新的高质量曲面细分算法,都依赖于由 n>4 个四边形包围的网格节点向非常点的缓慢收敛。缓慢收敛相当于 λ>0.5 的收缩比。为了改善形状,防止参数化与表面生长不协调,或改善非常点附近等几何分析的收敛性,许多算法通过改变细化规则来明确调整 λ。然而,迄今为止,这种对 λ 的调整导致了较差的表面质量,表现为高亮线的不均匀分布或摆动。最近的二次吸引细分法(QAS)基于对中心点二次展开的谨慎选择,生成高质量、有约束曲率的曲面,并且与 Catmull-Clark 细分法一样,通过矩阵乘法创建下一个细分环的控制点。但当 n>4 时,QAS 与 Catmull-Clark 细分的收缩率 λCC>1/2 相同。当 n=5,...,10 时,与 QAS 相比,QAS+ 提高了对二元域细化的统一 λ=12 的收敛性,且不影响曲面质量。

Classic generalized subdivision, such as Catmull–Clark subdivision, as well as recent subdivision algorithms for high-quality surfaces, rely on slower convergence towards extraordinary points for mesh nodes surrounded by quadrilaterals. Slow convergence corresponds to a contraction-ratio of . To improve shape, prevent parameterization discordant with surface growth, or to improve convergence in isogeometric analysis near extraordinary points, a number of algorithms explicitly adjust by altering refinement rules. However, such tuning of has so far led to poorer surface quality, visible as uneven distribution or oscillation of highlight lines. The recent Quadratic-Attraction Subdivision (QAS) generates high-quality, bounded curvature surfaces based on a careful choice of quadratic expansion at the central point and, just like Catmull–Clark subdivision, creates the control points of the next subdivision ring by matrix multiplication. But QAS shares the contraction-ratio of Catmull–Clark subdivision when . For , QAS improves the convergence to the uniform of binary domain refinement and without sacrificing surface quality compared to QAS.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


