连续 -1$-1$超几何正交多项式

IF 2.6 2区数学 Q1 MATHEMATICS, APPLIED

Studies in Applied Mathematics Pub Date : 2024-07-04 DOI:10.1111/sapm.12728

Jonathan Pelletier, Luc Vinet, Alexei Zhedanov

{"title":"连续 -1$-1$超几何正交多项式","authors":"Jonathan Pelletier, Luc Vinet, Alexei Zhedanov","doi":"10.1111/sapm.12728","DOIUrl":null,"url":null,"abstract":"The study of <math>\n <semantics>\n <mrow>\n <mo>−</mo>\n <mn>1</mn>\n </mrow>\n <annotation>$-1$</annotation>\n </semantics></math> orthogonal polynomials viewed as <math>\n <semantics>\n <mrow>\n <mi>q</mi>\n <mo>→</mo>\n <mo>−</mo>\n <mn>1</mn>\n </mrow>\n <annotation>$q\\rightarrow -1$</annotation>\n </semantics></math> limits of the <math>\n <semantics>\n <mi>q</mi>\n <annotation>$q$</annotation>\n </semantics></math>-orthogonal polynomials is pursued. This paper presents the continuous polynomials part of the <math>\n <semantics>\n <mrow>\n <mo>−</mo>\n <mn>1</mn>\n </mrow>\n <annotation>$-1$</annotation>\n </semantics></math> analog of the <math>\n <semantics>\n <mi>q</mi>\n <annotation>$q$</annotation>\n </semantics></math>-Askey scheme. A compendium of the properties of all the continuous <math>\n <semantics>\n <mrow>\n <mo>−</mo>\n <mn>1</mn>\n </mrow>\n <annotation>$-1$</annotation>\n </semantics></math> hypergeometric polynomials and their connections is provided.","PeriodicalId":51174,"journal":{"name":"Studies in Applied Mathematics","volume":"153 3","pages":""},"PeriodicalIF":2.6000,"publicationDate":"2024-07-04","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1111/sapm.12728","citationCount":"0","resultStr":"{\"title\":\"Continuous \\n \\n \\n −\\n 1\\n \\n $-1$\\n hypergeometric orthogonal polynomials\",\"authors\":\"Jonathan Pelletier, Luc Vinet, Alexei Zhedanov\",\"doi\":\"10.1111/sapm.12728\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"The study of <math>\\n <semantics>\\n <mrow>\\n <mo>−</mo>\\n <mn>1</mn>\\n </mrow>\\n <annotation>$-1$</annotation>\\n </semantics></math> orthogonal polynomials viewed as <math>\\n <semantics>\\n <mrow>\\n <mi>q</mi>\\n <mo>→</mo>\\n <mo>−</mo>\\n <mn>1</mn>\\n </mrow>\\n <annotation>$q\\\\rightarrow -1$</annotation>\\n </semantics></math> limits of the <math>\\n <semantics>\\n <mi>q</mi>\\n <annotation>$q$</annotation>\\n </semantics></math>-orthogonal polynomials is pursued. This paper presents the continuous polynomials part of the <math>\\n <semantics>\\n <mrow>\\n <mo>−</mo>\\n <mn>1</mn>\\n </mrow>\\n <annotation>$-1$</annotation>\\n </semantics></math> analog of the <math>\\n <semantics>\\n <mi>q</mi>\\n <annotation>$q$</annotation>\\n </semantics></math>-Askey scheme. A compendium of the properties of all the continuous <math>\\n <semantics>\\n <mrow>\\n <mo>−</mo>\\n <mn>1</mn>\\n </mrow>\\n <annotation>$-1$</annotation>\\n </semantics></math> hypergeometric polynomials and their connections is provided.\",\"PeriodicalId\":51174,\"journal\":{\"name\":\"Studies in Applied Mathematics\",\"volume\":\"153 3\",\"pages\":\"\"},\"PeriodicalIF\":2.6000,\"publicationDate\":\"2024-07-04\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1111/sapm.12728\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Studies in Applied Mathematics\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1111/sapm.12728\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS, APPLIED\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Studies in Applied Mathematics","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1111/sapm.12728","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS, APPLIED","Score":null,"Total":0}

引用次数: 0

摘要

正交多项式的研究被视为-正交多项式的极限。本文介绍了-Askey 方案类比的连续多项式部分。本文概述了所有连续超几何多项式的性质及其联系。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

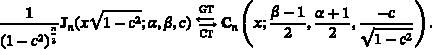
Continuous

−
1

$-1$
hypergeometric orthogonal polynomials

查看原文本刊更多论文

Continuous − 1 $-1$ hypergeometric orthogonal polynomials

The study of $- 1$ orthogonal polynomials viewed as $q \to - 1$ limits of the $q$ -orthogonal polynomials is pursued. This paper presents the continuous polynomials part of the $- 1$ analog of the $q$ -Askey scheme. A compendium of the properties of all the continuous $- 1$ hypergeometric polynomials and their connections is provided.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Studies in Applied Mathematics 数学-应用数学

CiteScore

4.30

自引率

3.70%

发文量

审稿时长

>12 weeks

期刊介绍： Studies in Applied Mathematics explores the interplay between mathematics and the applied disciplines. It publishes papers that advance the understanding of physical processes, or develop new mathematical techniques applicable to physical and real-world problems. Its main themes include (but are not limited to) nonlinear phenomena, mathematical modeling, integrable systems, asymptotic analysis, inverse problems, numerical analysis, dynamical systems, scientific computing and applications to areas such as fluid mechanics, mathematical biology, and optics.