整数分区网格中的箭头关系

IF 3.2 3区计算机科学 Q2 COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCE

International Journal of Approximate Reasoning Pub Date : 2024-06-27 DOI:10.1016/j.ijar.2024.109244

Asma'a Almazaydeh , Mike Behrisch , Edith Vargas-García , Andreas Wachtel

引用次数: 0

摘要

我们给出了任意正整数 n 的分格 Ln 的标准上下文 K(Ln) 在支配阶下的单箭头和双箭头关系的完整特征，从而解决了甘特 2020/2022 年的一个未决问题。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

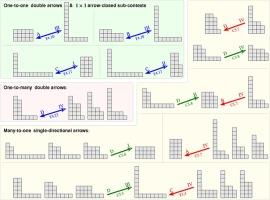
Arrow relations in lattices of integer partitions

查看原文本刊更多论文

Arrow relations in lattices of integer partitions

We give a complete characterisation of the single and double arrow relations of the standard context $K (L_{n})$ of the lattice $L_{n}$ of partitions of any positive integer n under the dominance order, thereby addressing an open question of Ganter, 2020/2022.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

International Journal of Approximate Reasoning 工程技术-计算机：人工智能

CiteScore

6.90

自引率

12.80%

发文量

170

审稿时长

67 days

期刊介绍： The International Journal of Approximate Reasoning is intended to serve as a forum for the treatment of imprecision and uncertainty in Artificial and Computational Intelligence, covering both the foundations of uncertainty theories, and the design of intelligent systems for scientific and engineering applications. It publishes high-quality research papers describing theoretical developments or innovative applications, as well as review articles on topics of general interest. Relevant topics include, but are not limited to, probabilistic reasoning and Bayesian networks, imprecise probabilities, random sets, belief functions (Dempster-Shafer theory), possibility theory, fuzzy sets, rough sets, decision theory, non-additive measures and integrals, qualitative reasoning about uncertainty, comparative probability orderings, game-theoretic probability, default reasoning, nonstandard logics, argumentation systems, inconsistency tolerant reasoning, elicitation techniques, philosophical foundations and psychological models of uncertain reasoning. Domains of application for uncertain reasoning systems include risk analysis and assessment, information retrieval and database design, information fusion, machine learning, data and web mining, computer vision, image and signal processing, intelligent data analysis, statistics, multi-agent systems, etc.