厄林电势微分方程

IF 1.6 4区物理与天体物理 Q3 PHYSICS, CONDENSED MATTER

The European Physical Journal B Pub Date : 2024-06-22 DOI:10.1140/epjb/s10051-024-00728-x

Alexei M. Frolov

{"title":"厄林电势微分方程","authors":"Alexei M. Frolov","doi":"10.1140/epjb/s10051-024-00728-x","DOIUrl":null,"url":null,"abstract":"The second-order differential equation for the Uehling potential is derived explicitly. The right side of this differential equation is a linear combination of the two Macdonald’s functions \\(K_{0}(b r)\\) and \\(K_{1}(b r)\\). This central potential is of great interest in many QED problems, since it describes the lowest order correction for vacuum polarization in few- and many-electron atoms, ions, muonic and bi-muonic atoms/ions as well as in other similar systems.","PeriodicalId":787,"journal":{"name":"The European Physical Journal B","volume":"97 6","pages":""},"PeriodicalIF":1.6000,"publicationDate":"2024-06-22","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Differential equation for the Uehling potential\",\"authors\":\"Alexei M. Frolov\",\"doi\":\"10.1140/epjb/s10051-024-00728-x\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"The second-order differential equation for the Uehling potential is derived explicitly. The right side of this differential equation is a linear combination of the two Macdonald’s functions \\\\(K_{0}(b r)\\\\) and \\\\(K_{1}(b r)\\\\). This central potential is of great interest in many QED problems, since it describes the lowest order correction for vacuum polarization in few- and many-electron atoms, ions, muonic and bi-muonic atoms/ions as well as in other similar systems.\",\"PeriodicalId\":787,\"journal\":{\"name\":\"The European Physical Journal B\",\"volume\":\"97 6\",\"pages\":\"\"},\"PeriodicalIF\":1.6000,\"publicationDate\":\"2024-06-22\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"The European Physical Journal B\",\"FirstCategoryId\":\"4\",\"ListUrlMain\":\"https://link.springer.com/article/10.1140/epjb/s10051-024-00728-x\",\"RegionNum\":4,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"PHYSICS, CONDENSED MATTER\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"The European Physical Journal B","FirstCategoryId":"4","ListUrlMain":"https://link.springer.com/article/10.1140/epjb/s10051-024-00728-x","RegionNum":4,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"PHYSICS, CONDENSED MATTER","Score":null,"Total":0}

引用次数: 0

摘要

摘要明确推导出了上林势的二阶微分方程。这个微分方程的右边是两个麦克唐纳函数\(K_{0}(b r)\)和\(K_{1}(b r)\)的线性组合。这个中心势在许多 QED 问题中都具有重大意义，因为它描述了少电子和多电子原子、离子、μ介子和双μ介子原子/离子以及其他类似系统中真空极化的最低阶修正。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

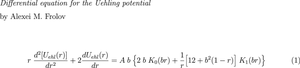
Differential equation for the Uehling potential

查看原文本刊更多论文

Differential equation for the Uehling potential

The second-order differential equation for the Uehling potential is derived explicitly. The right side of this differential equation is a linear combination of the two Macdonald’s functions \(K_{0}(b r)\) and \(K_{1}(b r)\). This central potential is of great interest in many QED problems, since it describes the lowest order correction for vacuum polarization in few- and many-electron atoms, ions, muonic and bi-muonic atoms/ions as well as in other similar systems.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

The European Physical Journal B 物理-物理：凝聚态物理

CiteScore

2.80

自引率

6.20%

发文量

184

审稿时长

5.1 months

期刊介绍： Solid State and Materials; Mesoscopic and Nanoscale Systems; Computational Methods; Statistical and Nonlinear Physics