单线性残差网格：公理化、品种和 FEP

IF 0.6 4区数学 Q3 MATHEMATICS

Algebra Universalis Pub Date : 2024-06-21 DOI:10.1007/s00012-024-00856-6

Nikolaos Galatos, Xiao Zhuang

{"title":"单线性残差网格：公理化、品种和 FEP","authors":"Nikolaos Galatos, Xiao Zhuang","doi":"10.1007/s00012-024-00856-6","DOIUrl":null,"url":null,"abstract":"<div><p>We characterize all residuated lattices that have height equal to 3 and show that the variety they generate has continuum-many subvarieties. More generally, we study unilinear residuated lattices: their lattice is a union of disjoint incomparable chains, with bounds added. We we give two general constructions of unilinear residuated lattices, provide an axiomatization and a proof-theoretic calculus for the variety they generate, and prove the finite model property for various subvarieties.</p></div>","PeriodicalId":50827,"journal":{"name":"Algebra Universalis","volume":"85 3","pages":""},"PeriodicalIF":0.6000,"publicationDate":"2024-06-21","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Unilinear residuated lattices: axiomatization, varieties and FEP\",\"authors\":\"Nikolaos Galatos, Xiao Zhuang\",\"doi\":\"10.1007/s00012-024-00856-6\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>We characterize all residuated lattices that have height equal to 3 and show that the variety they generate has continuum-many subvarieties. More generally, we study unilinear residuated lattices: their lattice is a union of disjoint incomparable chains, with bounds added. We we give two general constructions of unilinear residuated lattices, provide an axiomatization and a proof-theoretic calculus for the variety they generate, and prove the finite model property for various subvarieties.</p></div>\",\"PeriodicalId\":50827,\"journal\":{\"name\":\"Algebra Universalis\",\"volume\":\"85 3\",\"pages\":\"\"},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2024-06-21\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Algebra Universalis\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s00012-024-00856-6\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Algebra Universalis","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s00012-024-00856-6","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

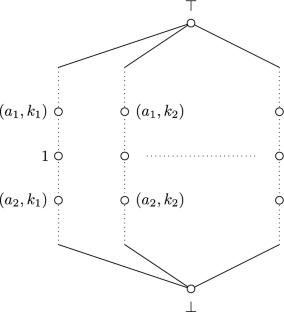
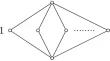
我们描述了所有高度等于 3 的残差格点的特征，并证明了它们生成的种类具有连续多子种类。更广义地说，我们研究的是单线性残差格：它们的格是不相交的不可比链的联合，并加上了边界。我们给出了单线性残差格的两个一般构造，为它们生成的综类提供了公理化和证明论的微积分，并证明了各种子综类的有限模型性质。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

Unilinear residuated lattices: axiomatization, varieties and FEP

查看原文本刊更多论文

Unilinear residuated lattices: axiomatization, varieties and FEP

We characterize all residuated lattices that have height equal to 3 and show that the variety they generate has continuum-many subvarieties. More generally, we study unilinear residuated lattices: their lattice is a union of disjoint incomparable chains, with bounds added. We we give two general constructions of unilinear residuated lattices, provide an axiomatization and a proof-theoretic calculus for the variety they generate, and prove the finite model property for various subvarieties.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Algebra Universalis 数学-数学

CiteScore

1.00

自引率

16.70%

发文量

审稿时长

3 months

期刊介绍： Algebra Universalis publishes papers in universal algebra, lattice theory, and related fields. In a pragmatic way, one could define the areas of interest of the journal as the union of the areas of interest of the members of the Editorial Board. In addition to research papers, we are also interested in publishing high quality survey articles.