学生对量子力学中特征值方程的理解:符号混合和感性分析
IF 3.6
2区 教育学
Q1 EDUCATION & EDUCATIONAL RESEARCH
Physical Review Physics Education Research
Pub Date : 2024-06-18
DOI:10.1103/physrevphyseducres.20.010153
引用次数: 0
摘要
在自旋第一量子力学课程中,为了考察学生从离散(自旋)系统到连续(位置)系统过渡期间的数学感知(MSM),要求学生构建一维位置算子的特征值方程。一部分回答采用了用狄拉克符号书写的特征值方程的一般形式。分析中使用了符号混合、符号形式和概念混合的组合以及 MSM 的分类框架。数据表明,特征值方程有两种不同的符号形式,它们共享一个符号模板,但具有不同的概念图式:一种是再现原式的变换,另一种是操作即行动。这些符号形式与两组情境知识相融合,构成了对特征值方程的三种不同解释的基础,并在此作为概念混合模型。本研究的分析是一个新颖的例子,初步证明了在自旋第一量子力学课程中,学生在从离散系统向连续系统过渡的过程中参与了感性认识活动。本文章由计算机程序翻译,如有差异,请以英文原文为准。
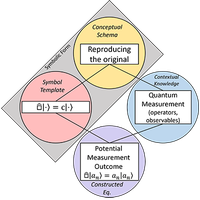
Student understanding of eigenvalue equations in quantum mechanics: Symbolic blending and sensemaking analysis
As part of an effort to examine students’ mathematical sensemaking (MSM) in a spins-first quantum mechanics course during the transition from discrete (spin) to continuous (position) systems, students were asked to construct an eigenvalue equation for a one-dimensional position operator. A subset of responses took the general form of an eigenvalue equation written in Dirac notation. Symbolic blending, a combination of symbolic forms and conceptual blending, as well as a categorical framework for MSM, were used in the analysis. The data suggest two different symbolic forms for an eigenvalue equation that share a symbol template but have distinct conceptual schemata: A transformation that reproduces the original and to operate is to act. These symbolic forms, when blended with two sets of contextual knowledge, form the basis of three different interpretations of eigenvalue equations modeled here as conceptual blends. The analysis in this study serves as a novel example of, and preliminary evidence for, student engagement in sensemaking activities in the transition from discrete to continuous systems in a spins-first quantum mechanics course.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Physical Review Physics Education Research
Social Sciences-Education
CiteScore
5.70
自引率
41.90%
发文量
84
审稿时长
32 weeks
期刊介绍:
PRPER covers all educational levels, from elementary through graduate education. All topics in experimental and theoretical physics education research are accepted, including, but not limited to:
Educational policy
Instructional strategies, and materials development
Research methodology
Epistemology, attitudes, and beliefs
Learning environment
Scientific reasoning and problem solving
Diversity and inclusion
Learning theory
Student participation
Faculty and teacher professional development
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


