翘曲积度量的谱常数刚性

IF 16.4 1区化学 Q1 CHEMISTRY, MULTIDISCIPLINARY

Accounts of Chemical Research Pub Date : 2024-06-30 DOI:10.1112/jlms.12958

Xiaoxiang Chai, Juncheol Pyo, Xueyuan Wan

{"title":"翘曲积度量的谱常数刚性","authors":"Xiaoxiang Chai, Juncheol Pyo, Xueyuan Wan","doi":"10.1112/jlms.12958","DOIUrl":null,"url":null,"abstract":"A theorem of Llarull says that if a smooth metric <math>\n <semantics>\n <mi>g</mi>\n <annotation>$g$</annotation>\n </semantics></math> on the <math>\n <semantics>\n <mi>n</mi>\n <annotation>$n$</annotation>\n </semantics></math>-sphere <math>\n <semantics>\n <msup>\n <mi>S</mi>\n <mi>n</mi>\n </msup>\n <annotation>$\\mathbb {S}^n$</annotation>\n </semantics></math> is bounded below by the standard round metric and the scalar curvature <math>\n <semantics>\n <msub>\n <mi>R</mi>\n <mi>g</mi>\n </msub>\n <annotation>$R_g$</annotation>\n </semantics></math> of <math>\n <semantics>\n <mi>g</mi>\n <annotation>$g$</annotation>\n </semantics></math> is bounded below by <math>\n <semantics>\n <mrow>\n <mi>n</mi>\n <mo>(</mo>\n <mi>n</mi>\n <mo>−</mo>\n <mn>1</mn>\n <mo>)</mo>\n </mrow>\n <annotation>$n (n - 1)$</annotation>\n </semantics></math>, then the metric <math>\n <semantics>\n <mi>g</mi>\n <annotation>$g$</annotation>\n </semantics></math> must be the standard round metric. We prove a spectral Llarull theorem by replacing the bound <math>\n <semantics>\n <mrow>\n <msub>\n <mi>R</mi>\n <mi>g</mi>\n </msub>\n <mo>⩾</mo>\n <mi>n</mi>\n <mrow>\n <mo>(</mo>\n <mi>n</mi>\n <mo>−</mo>\n <mn>1</mn>\n <mo>)</mo>\n </mrow>\n </mrow>\n <annotation>$R_g \\geqslant n (n - 1)$</annotation>\n </semantics></math> by a lower bound on the first eigenvalue of an elliptic operator involving the Laplacian and the scalar curvature <math>\n <semantics>\n <msub>\n <mi>R</mi>\n <mi>g</mi>\n </msub>\n <annotation>$R_g$</annotation>\n </semantics></math>. We utilize two methods: spinor and spacetime harmonic function.","PeriodicalId":1,"journal":{"name":"Accounts of Chemical Research","volume":null,"pages":null},"PeriodicalIF":16.4000,"publicationDate":"2024-06-30","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1112/jlms.12958","citationCount":"0","resultStr":"{\"title\":\"Spectral constant rigidity of warped product metrics\",\"authors\":\"Xiaoxiang Chai, Juncheol Pyo, Xueyuan Wan\",\"doi\":\"10.1112/jlms.12958\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"A theorem of Llarull says that if a smooth metric <math>\\n <semantics>\\n <mi>g</mi>\\n <annotation>$g$</annotation>\\n </semantics></math> on the <math>\\n <semantics>\\n <mi>n</mi>\\n <annotation>$n$</annotation>\\n </semantics></math>-sphere <math>\\n <semantics>\\n <msup>\\n <mi>S</mi>\\n <mi>n</mi>\\n </msup>\\n <annotation>$\\\\mathbb {S}^n$</annotation>\\n </semantics></math> is bounded below by the standard round metric and the scalar curvature <math>\\n <semantics>\\n <msub>\\n <mi>R</mi>\\n <mi>g</mi>\\n </msub>\\n <annotation>$R_g$</annotation>\\n </semantics></math> of <math>\\n <semantics>\\n <mi>g</mi>\\n <annotation>$g$</annotation>\\n </semantics></math> is bounded below by <math>\\n <semantics>\\n <mrow>\\n <mi>n</mi>\\n <mo>(</mo>\\n <mi>n</mi>\\n <mo>−</mo>\\n <mn>1</mn>\\n <mo>)</mo>\\n </mrow>\\n <annotation>$n (n - 1)$</annotation>\\n </semantics></math>, then the metric <math>\\n <semantics>\\n <mi>g</mi>\\n <annotation>$g$</annotation>\\n </semantics></math> must be the standard round metric. We prove a spectral Llarull theorem by replacing the bound <math>\\n <semantics>\\n <mrow>\\n <msub>\\n <mi>R</mi>\\n <mi>g</mi>\\n </msub>\\n <mo>⩾</mo>\\n <mi>n</mi>\\n <mrow>\\n <mo>(</mo>\\n <mi>n</mi>\\n <mo>−</mo>\\n <mn>1</mn>\\n <mo>)</mo>\\n </mrow>\\n </mrow>\\n <annotation>$R_g \\\\geqslant n (n - 1)$</annotation>\\n </semantics></math> by a lower bound on the first eigenvalue of an elliptic operator involving the Laplacian and the scalar curvature <math>\\n <semantics>\\n <msub>\\n <mi>R</mi>\\n <mi>g</mi>\\n </msub>\\n <annotation>$R_g$</annotation>\\n </semantics></math>. We utilize two methods: spinor and spacetime harmonic function.\",\"PeriodicalId\":1,\"journal\":{\"name\":\"Accounts of Chemical Research\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":16.4000,\"publicationDate\":\"2024-06-30\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1112/jlms.12958\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Accounts of Chemical Research\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1112/jlms.12958\",\"RegionNum\":1,\"RegionCategory\":\"化学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"CHEMISTRY, MULTIDISCIPLINARY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Accounts of Chemical Research","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1112/jlms.12958","RegionNum":1,"RegionCategory":"化学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"CHEMISTRY, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

摘要

拉鲁尔定理指出，如果 n $n$ -球面 S n $\mathbb {S}^n$ 上的光滑度量 g $g$ 的下界是标准圆度量，并且 g $g$ 的标量曲率 R g $R_g$ 的下界是 n ( n - 1 ) $n (n - 1)$ ，那么度量 g $g$ 一定是标准圆度量。我们将 R g ⩾ n ( n - 1 ) $R_g \geqslant n (n - 1)$ 约束替换为涉及拉普拉卡和标量曲率 R g $R_g$ 的椭圆算子的第一个特征值的下限，从而证明了谱拉鲁尔定理。我们采用两种方法：旋量和时空谐函数。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

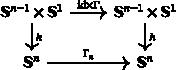
Spectral constant rigidity of warped product metrics

查看原文本刊更多论文

Spectral constant rigidity of warped product metrics

A theorem of Llarull says that if a smooth metric $g$ on the $n$ -sphere $S^{n}$ is bounded below by the standard round metric and the scalar curvature $R_{g}$ of $g$ is bounded below by $n (n - 1)$ , then the metric $g$ must be the standard round metric. We prove a spectral Llarull theorem by replacing the bound $R_{g} ⩾ n (n - 1)$ by a lower bound on the first eigenvalue of an elliptic operator involving the Laplacian and the scalar curvature $R_{g}$ . We utilize two methods: spinor and spacetime harmonic function.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Accounts of Chemical Research 化学-化学综合

CiteScore

31.40

自引率

1.10%

发文量

312

审稿时长

2 months

期刊介绍： Accounts of Chemical Research presents short, concise and critical articles offering easy-to-read overviews of basic research and applications in all areas of chemistry and biochemistry. These short reviews focus on research from the author’s own laboratory and are designed to teach the reader about a research project. In addition, Accounts of Chemical Research publishes commentaries that give an informed opinion on a current research problem. Special Issues online are devoted to a single topic of unusual activity and significance. Accounts of Chemical Research replaces the traditional article abstract with an article "Conspectus." These entries synopsize the research affording the reader a closer look at the content and significance of an article. Through this provision of a more detailed description of the article contents, the Conspectus enhances the article's discoverability by search engines and the exposure for the research.