团队语义的紧凑性

IF 0.4 4区数学 Q4 LOGIC

Mathematical Logic Quarterly Pub Date : 2024-05-27 DOI:10.1002/malq.202200072

Joni Puljujärvi, Davide Emilio Quadrellaro

{"title":"团队语义的紧凑性","authors":"Joni Puljujärvi, Davide Emilio Quadrellaro","doi":"10.1002/malq.202200072","DOIUrl":null,"url":null,"abstract":"<p>We provide two proofs of the compactness theorem for extensions of first-order logic based on team semantics. First, we build upon Lück's [16] ultraproduct construction for team semantics and prove a suitable version of Łoś' Theorem. Second, we show that by working with suitably saturated models, we can generalize the proof of Kontinen and Yang [13] to sets of formulas with arbitrarily many variables.</p>","PeriodicalId":49864,"journal":{"name":"Mathematical Logic Quarterly","volume":null,"pages":null},"PeriodicalIF":0.4000,"publicationDate":"2024-05-27","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1002/malq.202200072","citationCount":"0","resultStr":"{\"title\":\"Compactness in team semantics\",\"authors\":\"Joni Puljujärvi, Davide Emilio Quadrellaro\",\"doi\":\"10.1002/malq.202200072\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>We provide two proofs of the compactness theorem for extensions of first-order logic based on team semantics. First, we build upon Lück's [16] ultraproduct construction for team semantics and prove a suitable version of Łoś' Theorem. Second, we show that by working with suitably saturated models, we can generalize the proof of Kontinen and Yang [13] to sets of formulas with arbitrarily many variables.</p>\",\"PeriodicalId\":49864,\"journal\":{\"name\":\"Mathematical Logic Quarterly\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.4000,\"publicationDate\":\"2024-05-27\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1002/malq.202200072\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Mathematical Logic Quarterly\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1002/malq.202200072\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"LOGIC\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Mathematical Logic Quarterly","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1002/malq.202200072","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"LOGIC","Score":null,"Total":0}

引用次数: 0

摘要

我们为基于团队语义的一阶逻辑扩展提供了两个紧凑性定理证明。首先，我们以 Lück [16] 的团队语义超积构造为基础，证明了一个合适版本的 Łoś' Theorem。其次，我们证明了通过使用合适的饱和模型，我们可以将 Kontinen 和 Yang [13] 的证明推广到具有任意多变量的公式集。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

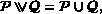
Compactness in team semantics

查看原文本刊更多论文

Compactness in team semantics

We provide two proofs of the compactness theorem for extensions of first-order logic based on team semantics. First, we build upon Lück's [16] ultraproduct construction for team semantics and prove a suitable version of Łoś' Theorem. Second, we show that by working with suitably saturated models, we can generalize the proof of Kontinen and Yang [13] to sets of formulas with arbitrarily many variables.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Mathematical Logic Quarterly 数学-数学

CiteScore

0.60

自引率

0.00%

发文量

审稿时长

>12 weeks

期刊介绍： Mathematical Logic Quarterly publishes original contributions on mathematical logic and foundations of mathematics and related areas, such as general logic, model theory, recursion theory, set theory, proof theory and constructive mathematics, algebraic logic, nonstandard models, and logical aspects of theoretical computer science.