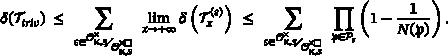
Quadratic forms and Genus Theory: A link with 2-descent and an application to nontrivial specializations of ideal classes

Genus Theory is a classical feature of integral binary quadratic forms. Using the author's generalization of the well-known correspondence between quadratic form classes and ideal classes of quadratic algebras, we extend it to the case when quadratic forms are twisted and have coefficients in any principal ideal domain (PID) $R$. When $R=K\left[X\right]$, we show that the Genus Theory map is the quadratic form version of the 2-descent map on a certain hyperelliptic curve. As an application, we make a contribution to a question of Agboola and Pappas regarding a specialization problem of divisor classes on hyperelliptic curves. Under suitable assumptions, we prove that the set of nontrivial specializations has density 1.