多尺度增强型非均匀变换场分析

IF 2.7 3区工程技术 Q1 ENGINEERING, MULTIDISCIPLINARY

International Journal for Numerical Methods in Engineering Pub Date : 2024-05-13 DOI:10.1002/nme.7501

A. Mishra, P. Carrara, S. Marfia, E. Sacco, L. De Lorenzis

{"title":"多尺度增强型非均匀变换场分析","authors":"A. Mishra, P. Carrara, S. Marfia, E. Sacco, L. De Lorenzis","doi":"10.1002/nme.7501","DOIUrl":null,"url":null,"abstract":"Enhanced transformation field analysis (E-TFA), recently proposed for reduced-order modeling, is here formulated for and applied to multiscale analysis. The approach is able to reproduce a highly complex nonlinear macroscale behavior, resulting from a microstructure with cohesive interfaces embedded in an elasto-plastic bulk. E-TFA features a consistent tangent matrix in its solution procedure, which enables a straightforward definition of the upscaled tangent stiffness tensor. Numerical tests show that, compared to FE<math>\n <semantics>\n <mrow>\n <msup>\n <mo> </mo>\n <mrow>\n <mn>2</mn>\n </mrow>\n </msup>\n </mrow>\n <annotation>$$ {}^2 $$</annotation>\n </semantics></math>, the proposed approach yields accurate solutions at a lower computational cost.","PeriodicalId":13699,"journal":{"name":"International Journal for Numerical Methods in Engineering","volume":null,"pages":null},"PeriodicalIF":2.7000,"publicationDate":"2024-05-13","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1002/nme.7501","citationCount":"0","resultStr":"{\"title\":\"Multiscale enhanced non-uniform transformation field analysis\",\"authors\":\"A. Mishra, P. Carrara, S. Marfia, E. Sacco, L. De Lorenzis\",\"doi\":\"10.1002/nme.7501\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"Enhanced transformation field analysis (E-TFA), recently proposed for reduced-order modeling, is here formulated for and applied to multiscale analysis. The approach is able to reproduce a highly complex nonlinear macroscale behavior, resulting from a microstructure with cohesive interfaces embedded in an elasto-plastic bulk. E-TFA features a consistent tangent matrix in its solution procedure, which enables a straightforward definition of the upscaled tangent stiffness tensor. Numerical tests show that, compared to FE<math>\\n <semantics>\\n <mrow>\\n <msup>\\n <mo> </mo>\\n <mrow>\\n <mn>2</mn>\\n </mrow>\\n </msup>\\n </mrow>\\n <annotation>$$ {}^2 $$</annotation>\\n </semantics></math>, the proposed approach yields accurate solutions at a lower computational cost.\",\"PeriodicalId\":13699,\"journal\":{\"name\":\"International Journal for Numerical Methods in Engineering\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":2.7000,\"publicationDate\":\"2024-05-13\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1002/nme.7501\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"International Journal for Numerical Methods in Engineering\",\"FirstCategoryId\":\"5\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1002/nme.7501\",\"RegionNum\":3,\"RegionCategory\":\"工程技术\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"ENGINEERING, MULTIDISCIPLINARY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"International Journal for Numerical Methods in Engineering","FirstCategoryId":"5","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1002/nme.7501","RegionNum":3,"RegionCategory":"工程技术","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"ENGINEERING, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

摘要

增强变换场分析法（E-TFA）是最近针对降阶建模提出的一种方法，本文将其应用于多尺度分析。该方法能够再现高度复杂的非线性宏观尺度行为，这种行为是由嵌入弹性塑性体中的具有内聚界面的微结构引起的。E-TFA 在其求解过程中采用了一致的正切矩阵，从而可以直接定义放大的正切刚度张量。数值测试表明，与 FE 相比，所提出的方法能以较低的计算成本获得精确的求解。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

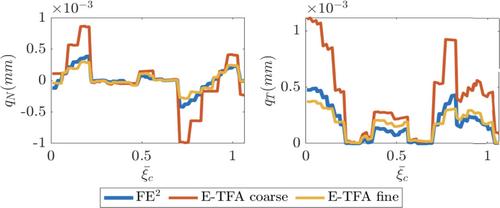
Multiscale enhanced non-uniform transformation field analysis

查看原文本刊更多论文

Multiscale enhanced non-uniform transformation field analysis

Enhanced transformation field analysis (E-TFA), recently proposed for reduced-order modeling, is here formulated for and applied to multiscale analysis. The approach is able to reproduce a highly complex nonlinear macroscale behavior, resulting from a microstructure with cohesive interfaces embedded in an elasto-plastic bulk. E-TFA features a consistent tangent matrix in its solution procedure, which enables a straightforward definition of the upscaled tangent stiffness tensor. Numerical tests show that, compared to FE $^{2}$ , the proposed approach yields accurate solutions at a lower computational cost.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

International Journal for Numerical Methods in Engineering 工程技术-工程：综合

CiteScore

5.70

自引率

6.90%

发文量

276

审稿时长

5.3 months

期刊介绍： The International Journal for Numerical Methods in Engineering publishes original papers describing significant, novel developments in numerical methods that are applicable to engineering problems. The Journal is known for welcoming contributions in a wide range of areas in computational engineering, including computational issues in model reduction, uncertainty quantification, verification and validation, inverse analysis and stochastic methods, optimisation, element technology, solution techniques and parallel computing, damage and fracture, mechanics at micro and nano-scales, low-speed fluid dynamics, fluid-structure interaction, electromagnetics, coupled diffusion phenomena, and error estimation and mesh generation. It is emphasized that this is by no means an exhaustive list, and particularly papers on multi-scale, multi-physics or multi-disciplinary problems, and on new, emerging topics are welcome.