对偶巴拿赫代数的弱可配性

IF 0.7 3区数学 Q2 MATHEMATICS

Proceedings of the Edinburgh Mathematical Society Pub Date : 2024-04-29 DOI:10.1017/s0013091524000300

Amin Mahmoodi

引用次数: 0

摘要

我们定义并研究了对偶巴拿赫代数的一个合适的弱可亲和性概念，我们称之为弱康恩可亲和性。除其他外，我们还证明了局部紧凑群 G 的度量代数 M(G) 总是弱康恩可亲和性的。它可以作为约翰逊关于 $L^1(G)$ 总是弱可朋性定理的补充[10]。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

查看原文本刊更多论文

Weak amenability for dual Banach algebras

A suitable notion of weak amenability for dual Banach algebras, which we call weak Connes amenability, is defined and studied. Among other things, it is proved that the measure algebra M(G) of a locally compact group G is always weakly Connes amenable. It can be a complement to Johnson’s theorem that 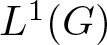$L^1(G)$ is always weakly amenable [10].

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Proceedings of the Edinburgh Mathematical Society 数学-数学

CiteScore

1.10

自引率

0.00%

发文量

审稿时长

6 months

期刊介绍： The Edinburgh Mathematical Society was founded in 1883 and over the years, has evolved into the principal society for the promotion of mathematics research in Scotland. The Society has published its Proceedings since 1884. This journal contains research papers on topics in a broad range of pure and applied mathematics, together with a number of topical book reviews.