对数唐纳森-托马斯理论
IF 2.9
1区 数学
Q1 MATHEMATICS
引用次数: 0
摘要
我们构建了唐纳森-托马斯(Donaldson-Thomas)理论的$(X|D)$对,枚举了 X 上相对于 D 的理想卷。我们提出了与标准理论平行的准时评估、合理性和穿墙猜想。当被除数是光滑的时候,我们的形式主义专攻于相对理想剪切的李-吴理论,并与最近关于对数格罗莫夫-维滕理论与展开的研究并行。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Logarithmic Donaldson–Thomas theory
Let X be a smooth and projective threefold with a simple normal crossings divisor D. We construct the Donaldson–Thomas theory of the pair 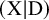 $(X|D)$ enumerating ideal sheaves on X relative to D. These moduli spaces are compactified by studying subschemes in expansions of the target geometry, and the moduli space carries a virtual fundamental class leading to numerical invariants with expected properties. We formulate punctual evaluation, rationality and wall-crossing conjectures, in parallel with the standard theory. Our formalism specializes to the Li–Wu theory of relative ideal sheaves when the divisor is smooth and is parallel to recent work on logarithmic Gromov–Witten theory with expansions.
$(X|D)$ enumerating ideal sheaves on X relative to D. These moduli spaces are compactified by studying subschemes in expansions of the target geometry, and the moduli space carries a virtual fundamental class leading to numerical invariants with expected properties. We formulate punctual evaluation, rationality and wall-crossing conjectures, in parallel with the standard theory. Our formalism specializes to the Li–Wu theory of relative ideal sheaves when the divisor is smooth and is parallel to recent work on logarithmic Gromov–Witten theory with expansions.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Forum of Mathematics Pi
Mathematics-Statistics and Probability
CiteScore
3.50
自引率
0.00%
发文量
21
审稿时长
19 weeks
期刊介绍:
Forum of Mathematics, Pi is the open access alternative to the leading generalist mathematics journals and are of real interest to a broad cross-section of all mathematicians. Papers published are of the highest quality.
Forum of Mathematics, Pi and Forum of Mathematics, Sigma are an exciting new development in journal publishing. Together they offer fully open access publication combined with peer-review standards set by an international editorial board of the highest calibre, and all backed by Cambridge University Press and our commitment to quality. Strong research papers from all parts of pure mathematics and related areas are welcomed. All published papers are free online to readers in perpetuity.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


