希尔兹布吕赫表面的 0 属对数和热带定域计数
IF 1
2区 数学
Q1 MATHEMATICS
Journal of the London Mathematical Society-Second Series
Pub Date : 2024-03-27
DOI:10.1112/jlms.12892
引用次数: 0
摘要
对于非星状投影环 variety X $X$ 而言,虚拟对数特维列夫度数被定义为对数稳定映射 M ¯ Γ ( X ) $overline{\mathcal {M}}_{mathsf {\Gamma }}(X)$ 到乘积 M ¯ g , n × X n $\overline{\mathcal {M}}_{g,n} 的变形的虚拟度数。\times X^n$ 。在本文中,我们在证明米哈尔金对应定理在对数虚拟特维列夫度数的 0 属中成立之后,使用热带方法为 X $X$ 是希尔泽布鲁赫曲面的情况提供了封闭公式。为此,我们明确列出了所有有助于计数的热带曲线。本文章由计算机程序翻译,如有差异,请以英文原文为准。
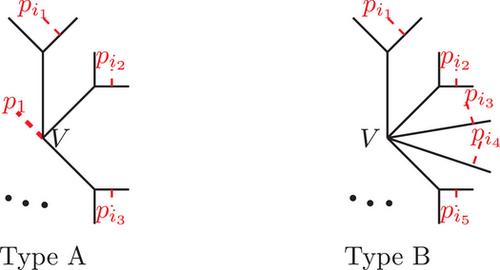
Genus 0 logarithmic and tropical fixed-domain counts for Hirzebruch surfaces
For a non-singular projective toric variety , the virtual logarithmic Tevelev degrees are defined as the virtual degree of the morphism from the moduli stack of logarithmic stable maps to the product . In this paper, after proving that Mikhalkin's correspondence theorem holds in genus 0 for logarithmic virtual Tevelev degrees, we use tropical methods to provide closed formulas for the case in which is a Hirzebruch surface. In order to do so, we explicitly list all the tropical curves contributing to the count.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.90
自引率
0.00%
发文量
186
审稿时长
6-12 weeks
期刊介绍:
The Journal of the London Mathematical Society has been publishing leading research in a broad range of mathematical subject areas since 1926. The Journal welcomes papers on subjects of general interest that represent a significant advance in mathematical knowledge, as well as submissions that are deemed to stimulate new interest and research activity.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


