1+1$$ 维中的邓克尔-福克-普朗克方程

IF 1.7 4区物理与天体物理 Q2 PHYSICS, MULTIDISCIPLINARY

Few-Body Systems Pub Date : 2024-03-14 DOI:10.1007/s00601-024-01898-1

R. D. Mota, D. Ojeda-Guillén, M. A. Xicoténcatl

引用次数: 0

摘要

通过用邓克尔导数代替空间导数，我们将福克-普朗克方程推广到 (1+1) 维。我们得到了邓克尔-福克-普朗克特征值方程，并对谐振子加上离心型势能进行了求解。此外，当漂移函数为奇数时，我们将结果还原为最近发展的维格纳-邓克尔超对称性的结果。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

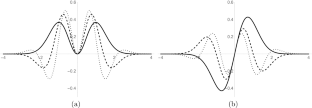
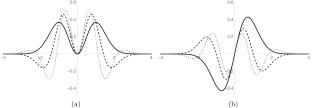
$The Dunkl–Fokker–Planck Equation in $1+1$ Dimensions$

查看原文本刊更多论文

The Dunkl–Fokker–Planck Equation in $1+1$ Dimensions

By replacing the spatial derivative with the Dunkl derivative, we generalize the Fokker-Planck equation in (1+1) dimensions. We obtain the Dunkl–Fokker–Planck eigenvalues equation and solve it for the harmonic oscillator plus a centrifugal-type potential. Furthermore, when the drift function is odd, we reduce our results to those of the recently developed Wigner–Dunkl supersymmetry.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Few-Body Systems 物理-物理：综合

CiteScore

2.90

自引率

18.80%

发文量

审稿时长

6-12 weeks

期刊介绍： The journal Few-Body Systems presents original research work – experimental, theoretical and computational – investigating the behavior of any classical or quantum system consisting of a small number of well-defined constituent structures. The focus is on the research methods, properties, and results characteristic of few-body systems. Examples of few-body systems range from few-quark states, light nuclear and hadronic systems; few-electron atomic systems and small molecules; and specific systems in condensed matter and surface physics (such as quantum dots and highly correlated trapped systems), up to and including large-scale celestial structures. Systems for which an equivalent one-body description is available or can be designed, and large systems for which specific many-body methods are needed are outside the scope of the journal. The journal is devoted to the publication of all aspects of few-body systems research and applications. While concentrating on few-body systems well-suited to rigorous solutions, the journal also encourages interdisciplinary contributions that foster common approaches and insights, introduce and benchmark the use of novel tools (e.g. machine learning) and develop relevant applications (e.g. few-body aspects in quantum technologies).