不具有准球或有界偏心特性的双曲空间实例
IF 0.4
4区 数学
Q3 MATHEMATICS
引用次数: 0
摘要
在本论文中,我们举例说明了非准大地构造空间,这些空间是双曲的(即满足格罗莫夫的 $4$ 点条件),而其中任意两个度量球的交点既不 "像 "一个球,也不具有均匀有界的偏心率。这回答了查特吉和尼布罗提出的一个公开问题。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Examples of hyperbolic spaces without the properties of quasi-ball or bounded eccentricity
In this note, we present examples of non-quasi-geodesic metric spaces which are hyperbolic (i.e., satisfying Gromov’s 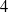 $4$-point condition) while the intersection of any two metric balls therein does not either ‘look like’ a ball or has uniformly bounded eccentricity. This answers an open question posed by Chatterji and Niblo.
$4$-point condition) while the intersection of any two metric balls therein does not either ‘look like’ a ball or has uniformly bounded eccentricity. This answers an open question posed by Chatterji and Niblo.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.10
自引率
0.00%
发文量
36
审稿时长
6-12 weeks
期刊介绍:
Glasgow Mathematical Journal publishes original research papers in any branch of pure and applied mathematics. An international journal, its policy is to feature a wide variety of research areas, which in recent issues have included ring theory, group theory, functional analysis, combinatorics, differential equations, differential geometry, number theory, algebraic topology, and the application of such methods in applied mathematics.
The journal has a web-based submission system for articles. For details of how to to upload your paper see GMJ - Online Submission Guidelines or go directly to the submission site.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


