用相对交映同调表征重度

IF 0.8 2区数学 Q2 MATHEMATICS

Journal of Topology Pub Date : 2024-03-09 DOI:10.1112/topo.12327

Cheuk Yu Mak, Yuhan Sun, Umut Varolgunes

{"title":"用相对交映同调表征重度","authors":"Cheuk Yu Mak, Yuhan Sun, Umut Varolgunes","doi":"10.1112/topo.12327","DOIUrl":null,"url":null,"abstract":"<p>For a compact subset <math>\n <semantics>\n <mi>K</mi>\n <annotation>$K$</annotation>\n </semantics></math> of a closed symplectic manifold <math>\n <semantics>\n <mrow>\n <mo>(</mo>\n <mi>M</mi>\n <mo>,</mo>\n <mi>ω</mi>\n <mo>)</mo>\n </mrow>\n <annotation>$(M, \\omega)$</annotation>\n </semantics></math>, we prove that <math>\n <semantics>\n <mi>K</mi>\n <annotation>$K$</annotation>\n </semantics></math> is heavy if and only if its relative symplectic cohomology over the Novikov field is nonzero. As an application, we show that if two compact sets are not heavy and Poisson commuting, then their union is also not heavy. A discussion on superheaviness together with some partial results is also included.</p>","PeriodicalId":56114,"journal":{"name":"Journal of Topology","volume":"17 1","pages":""},"PeriodicalIF":0.8000,"publicationDate":"2024-03-09","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1112/topo.12327","citationCount":"0","resultStr":"{\"title\":\"A characterization of heaviness in terms of relative symplectic cohomology\",\"authors\":\"Cheuk Yu Mak, Yuhan Sun, Umut Varolgunes\",\"doi\":\"10.1112/topo.12327\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>For a compact subset <math>\\n <semantics>\\n <mi>K</mi>\\n <annotation>$K$</annotation>\\n </semantics></math> of a closed symplectic manifold <math>\\n <semantics>\\n <mrow>\\n <mo>(</mo>\\n <mi>M</mi>\\n <mo>,</mo>\\n <mi>ω</mi>\\n <mo>)</mo>\\n </mrow>\\n <annotation>$(M, \\\\omega)$</annotation>\\n </semantics></math>, we prove that <math>\\n <semantics>\\n <mi>K</mi>\\n <annotation>$K$</annotation>\\n </semantics></math> is heavy if and only if its relative symplectic cohomology over the Novikov field is nonzero. As an application, we show that if two compact sets are not heavy and Poisson commuting, then their union is also not heavy. A discussion on superheaviness together with some partial results is also included.</p>\",\"PeriodicalId\":56114,\"journal\":{\"name\":\"Journal of Topology\",\"volume\":\"17 1\",\"pages\":\"\"},\"PeriodicalIF\":0.8000,\"publicationDate\":\"2024-03-09\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1112/topo.12327\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Topology\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1112/topo.12327\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Topology","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1112/topo.12327","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

对于封闭交映流形 ( M , ω ) $(M, \omega)$ 的紧凑子集 K $K$ ，我们证明当且仅当 K $K$ 在诺维科夫场上的相对交映同调非零时，K $K$ 是重的。作为应用，我们证明了如果两个紧凑集不重且泊松换向，那么它们的联合也不重。此外，我们还讨论了超重性以及一些局部结果。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

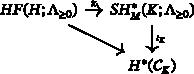
A characterization of heaviness in terms of relative symplectic cohomology

查看原文本刊更多论文

A characterization of heaviness in terms of relative symplectic cohomology

For a compact subset $K$ of a closed symplectic manifold $(M, ω)$ , we prove that $K$ is heavy if and only if its relative symplectic cohomology over the Novikov field is nonzero. As an application, we show that if two compact sets are not heavy and Poisson commuting, then their union is also not heavy. A discussion on superheaviness together with some partial results is also included.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Topology 数学-数学

CiteScore

2.00

自引率

9.10%

发文量

审稿时长

>12 weeks

期刊介绍： The Journal of Topology publishes papers of high quality and significance in topology, geometry and adjacent areas of mathematics. Interesting, important and often unexpected links connect topology and geometry with many other parts of mathematics, and the editors welcome submissions on exciting new advances concerning such links, as well as those in the core subject areas of the journal. The Journal of Topology was founded in 2008. It is published quarterly with articles published individually online prior to appearing in a printed issue.