关于与有磁场的薛定谔方程相关的平方和算子

IF 1 3区数学 Q1 MATHEMATICS

Annali di Matematica Pura ed Applicata Pub Date : 2024-03-07 DOI:10.1007/s10231-024-01434-2

Antonio Bove, Gregorio Chinni

{"title":"关于与有磁场的薛定谔方程相关的平方和算子","authors":"Antonio Bove, Gregorio Chinni","doi":"10.1007/s10231-024-01434-2","DOIUrl":null,"url":null,"abstract":"<div><p>We study the analytic and Gevrey regularity for a “sum of squares” operator closely connected to the Schrödinger equation with minimal coupling. We however assume that the (magnetic) vector potential has some degree of homogeneity and that the Hörmander bracket condition is satisfied. It is shown that the local analytic/Gevrey regularity of the solution is related to the multiplicities of the zeroes of the Lie bracket of the vector fields.</p></div>","PeriodicalId":8265,"journal":{"name":"Annali di Matematica Pura ed Applicata","volume":null,"pages":null},"PeriodicalIF":1.0000,"publicationDate":"2024-03-07","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"On a sum of squares operator related to the Schrödinger equation with a magnetic field\",\"authors\":\"Antonio Bove, Gregorio Chinni\",\"doi\":\"10.1007/s10231-024-01434-2\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>We study the analytic and Gevrey regularity for a “sum of squares” operator closely connected to the Schrödinger equation with minimal coupling. We however assume that the (magnetic) vector potential has some degree of homogeneity and that the Hörmander bracket condition is satisfied. It is shown that the local analytic/Gevrey regularity of the solution is related to the multiplicities of the zeroes of the Lie bracket of the vector fields.</p></div>\",\"PeriodicalId\":8265,\"journal\":{\"name\":\"Annali di Matematica Pura ed Applicata\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":1.0000,\"publicationDate\":\"2024-03-07\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Annali di Matematica Pura ed Applicata\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s10231-024-01434-2\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Annali di Matematica Pura ed Applicata","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s10231-024-01434-2","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

我们研究了与薛定谔方程密切相关的 "平方和 "算子的解析正则性和 Gevrey 正则性，其耦合度极小。然而，我们假设（磁）矢量势具有一定程度的同质性，并且满足赫曼德括号条件。研究表明，解的局部解析/杰弗里正则性与矢量场列括号零点的乘积有关。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

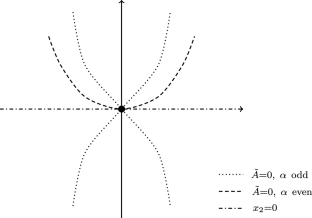
On a sum of squares operator related to the Schrödinger equation with a magnetic field

查看原文本刊更多论文

On a sum of squares operator related to the Schrödinger equation with a magnetic field

We study the analytic and Gevrey regularity for a “sum of squares” operator closely connected to the Schrödinger equation with minimal coupling. We however assume that the (magnetic) vector potential has some degree of homogeneity and that the Hörmander bracket condition is satisfied. It is shown that the local analytic/Gevrey regularity of the solution is related to the multiplicities of the zeroes of the Lie bracket of the vector fields.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Annali di Matematica Pura ed Applicata 数学-数学

CiteScore

2.10

自引率

10.00%

发文量

审稿时长

>12 weeks

期刊介绍： This journal, the oldest scientific periodical in Italy, was originally edited by Barnaba Tortolini and Francesco Brioschi and has appeared since 1850. Nowadays it is managed by a nonprofit organization, the Fondazione Annali di Matematica Pura ed Applicata, c.o. Dipartimento di Matematica "U. Dini", viale Morgagni 67A, 50134 Firenze, Italy, e-mail annali@math.unifi.it). A board of Italian university professors governs the Fondazione and appoints the editors of the journal, whose responsibility it is to supervise the refereeing process. The names of governors and editors appear on the front page of each issue. Their addresses appear in the title pages of each issue.