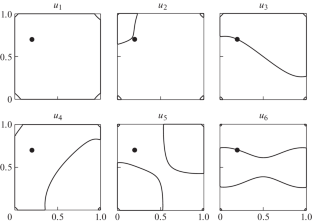
Finite Element Modeling of Eigenvibrations of a Square Plate with an Attached Oscillator

Abstract

A new symmetric linear variational statement is proposed for the problem of eigenvibrations of a plate with an attached oscillator. The existence of the sequence of positive eigenvalues of finite multiplicity with the limit point at infinity and the corresponding complete orthonormal system of eigenvectors is established. A new symmetric scheme of the finite element method with Hermite finite elements is stated. Error estimates consistent with the solution smoothness for the approximate eigenvalues and approximate eigenvectors are proved. The results of numerical experiments illustrating the influence of the smoothness of the solution on the computation accuracy are presented.