Toric 束的 Virasoro 约束条件

IF 2.8 1区数学 Q1 MATHEMATICS

Forum of Mathematics Pi Pub Date : 2024-01-01 DOI:10.1017/fmp.2024.2

Tom Coates, Alexander Givental, Hsian-Hua Tseng

{"title":"Toric 束的 Virasoro 约束条件","authors":"Tom Coates, Alexander Givental, Hsian-Hua Tseng","doi":"10.1017/fmp.2024.2","DOIUrl":null,"url":null,"abstract":"We show that the Virasoro conjecture in Gromov–Witten theory holds for the the total space of a toric bundle <img data-mimesubtype=\"png\" data-type=\"\" src=\"https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20240203073427923-0125:S2050508624000027:S2050508624000027_inline1.png\">$E \\to B$</img> if and only if it holds for the base B. The main steps are: (i) We establish a localization formula that expresses Gromov–Witten invariants of E, equivariant with respect to the fiberwise torus action in terms of genus-zero invariants of the toric fiber and all-genus invariants of B, and (ii) we pass to the nonequivariant limit in this formula, using Brown’s mirror theorem for toric bundles.","PeriodicalId":56024,"journal":{"name":"Forum of Mathematics Pi","volume":"29 1","pages":""},"PeriodicalIF":2.8000,"publicationDate":"2024-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Virasoro Constraints for Toric Bundles\",\"authors\":\"Tom Coates, Alexander Givental, Hsian-Hua Tseng\",\"doi\":\"10.1017/fmp.2024.2\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"We show that the Virasoro conjecture in Gromov–Witten theory holds for the the total space of a toric bundle <img data-mimesubtype=\\\"png\\\" data-type=\\\"\\\" src=\\\"https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20240203073427923-0125:S2050508624000027:S2050508624000027_inline1.png\\\">$E \\\\to B$</img> if and only if it holds for the base B. The main steps are: (i) We establish a localization formula that expresses Gromov–Witten invariants of E, equivariant with respect to the fiberwise torus action in terms of genus-zero invariants of the toric fiber and all-genus invariants of B, and (ii) we pass to the nonequivariant limit in this formula, using Brown’s mirror theorem for toric bundles.\",\"PeriodicalId\":56024,\"journal\":{\"name\":\"Forum of Mathematics Pi\",\"volume\":\"29 1\",\"pages\":\"\"},\"PeriodicalIF\":2.8000,\"publicationDate\":\"2024-01-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Forum of Mathematics Pi\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1017/fmp.2024.2\",\"RegionNum\":1,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Forum of Mathematics Pi","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1017/fmp.2024.2","RegionNum":1,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

我们证明了格罗莫夫-维滕理论中的维拉索罗猜想（Virasoro conjecture）在环束 $E \to B$ 的总空间中成立，前提是且仅当它在基 B 中成立时：(i) 我们建立了一个局部化公式，用环状纤维的零属不变式和 B 的全属不变式来表达 E 的格罗莫夫-维滕不变式，相对于纤维环状作用等变，以及 (ii) 我们利用布朗关于环状束的镜像定理来传递这个公式中的非变极限。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

查看原文本刊更多论文

Virasoro Constraints for Toric Bundles

We show that the Virasoro conjecture in Gromov–Witten theory holds for the the total space of a toric bundle 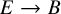$E \to B$ if and only if it holds for the base B. The main steps are: (i) We establish a localization formula that expresses Gromov–Witten invariants of E, equivariant with respect to the fiberwise torus action in terms of genus-zero invariants of the toric fiber and all-genus invariants of B, and (ii) we pass to the nonequivariant limit in this formula, using Brown’s mirror theorem for toric bundles.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Forum of Mathematics Pi Mathematics-Statistics and Probability

CiteScore

3.50

自引率

0.00%

发文量

审稿时长

19 weeks

期刊介绍： Forum of Mathematics, Pi is the open access alternative to the leading generalist mathematics journals and are of real interest to a broad cross-section of all mathematicians. Papers published are of the highest quality. Forum of Mathematics, Pi and Forum of Mathematics, Sigma are an exciting new development in journal publishing. Together they offer fully open access publication combined with peer-review standards set by an international editorial board of the highest calibre, and all backed by Cambridge University Press and our commitment to quality. Strong research papers from all parts of pure mathematics and related areas are welcomed. All published papers are free online to readers in perpetuity.